Глава двенадцатая. Тридцать разных задач

Я надеюсь, что знакомство с этой книжкой не прошло для читателя бесследно, что оно не только развлекло его, по и принесло известную пользу, развив его сметливость, находчивость, научив более умело распоряжаться своими знаниями. Читатель, вероятно, и сам желал бы теперь испытать на чем-нибудь свою сообразительность. Для этой цели и предназначаются те три десятка разнородных задач, которые собраны здесь, в последней главе нашей книжки.

101. Цепь.

Кузнецу принесли 5 обрывков цепи, по 3 звена в каждом обрывке, и заказали соединить их в одну цепь.

Рис. 91. Нить обрывков цепи

Прежде чем приняться за дело, кузнец стал думать, сколько колец понадобится для этого раскрыть и вновь заковать. Он решил, что придется раскрыть и снова заковать четыре кольца.

Нельзя ли, однако, выполнить работу, раскрыв, и заковав меньше колец?

102. Пауки и жуки.

Мальчик собрал в коробку пауков и жуков - всего 8 штук. Если пересчитать, сколько всех ног в коробке, то окажется 54 ноги.

Сколько же в коробке пауков и сколько жуков?

103. Плащ, шляпа и галоши.

Некто купил плащ, шляпу и галоши и заплатил за все 20 руб. Плащ стоит на 9 руб. больше, чем шляпа, а шляпа и плащ вместе на 16 руб. больше, чем галоши. Сколько стоит каждая вещь в отдельности?

Задачу требуется решить устным счетом, без уравнений.

104. Куриные и утиные яйца.

Корзины содержат яйца, в одних корзинах куриные яйца, в других - утиные. Число их 5, 6, 12, 14, 23 и 29. "Если я продам вот эту корзину, - размышляет продавец, - то у меня останется куриных яиц ровно вдвое больше, чем утиных." Какую корзину имел в виду продавец?

105. Перелет.

Самолет покрывает расстояние от города А до города В в 1 ч. 20 м. Однако обратный перелет он совершает в 80 мин. Как вы это объясните?

106. Денежные подарки.

Один отец дал своему сыну 150 руб., а другой своему - 100 руб. Оказалось, однако, что оба сына вместе увеличили свои капиталы только на 150 рублей. Чем это объяснить?

107. Две шашки.

На пустую шашечную доску надо поместить две шашки разного цвета. Сколько различных положений могут они занимать на доске?

108. Двумя цифрами.

Какое наименьшее целое положительное число можете вы написать двумя цифрами?

109. Единица.

Выразите 1, употребив все десять цифр.

110. Пятью девятками.

Выразите 10 пятью девятками. Укажите, по крайней мере, два способа.

111. Десятью цифрами.

Выразите 100, употребив все десять цифр. Сколькими способами можете вы это сделать? Существует не меньше четырех способов.

112. Четырьмя способами.

Четырьмя различными способами выразите 100 пятью одинаковыми цифрами.

113. Четырьмя единицами.

Какое самое большое число можете вы написать четырьмя единицами?

114. Загадочное деление.

В следующем примере деления все цифры заменены звездочками, кроме четырех четверок. Поставьте вместо звездочек те цифры, которые были заменены.

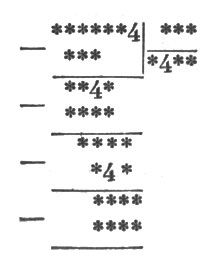
Задача эта имеет несколько различных решений.

115. Еще случай деления.

Сделайте то же с другим примером, в котором уцелело только семь семерок:

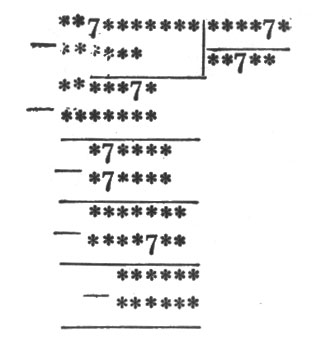
116. Что полуxится?

Сообразите в уме, на какую длину вытянется полоска, составленная из всех миллиметровых квадратиков одного квадратного метра, приложенных друг к другу вплотную.

117. В том же роде.

Сообразите в уме, на сколько километров возвышался бы столб, составленный из всех миллиметровых кубиков одного кубометра, положенных один на другой.

118. Самолет.

Самолет с размахом крыльев 12 м был сфотографирован во время полета снизу, когда он пролетал отвесно над аппаратом. Глубина камеры 12 см, размер изображения 8 мм.

На какой высоте летел самолет в момент фотографирования?

119. Миллион изделий.

Изделие весит 89,4 г. Сообразите в уме, сколько тонн весит миллион таких изделий.

120. Число путей.

На рис. 92 вы видите лесную дачу, разделенную просеками на квадратные кварталы. Пунктирной линией обозначен путь по просекам от точки А до точки В. Это, конечно, не единственный путь между указанными точками по просекам. Сколько можете вы насчитать различных путей одинаковой длины?

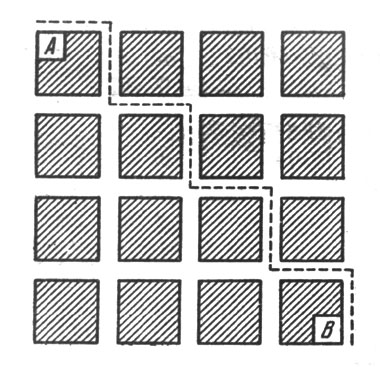
Рис. 92. Лесная дача разделена просеками

121. Циферблат.

Этот циферблат (рис. 93) надо разрезать на 6 частей любой формы, - так, однако, чтобы сумма чисел, имеющихся на каждом участке, была одна и та же.

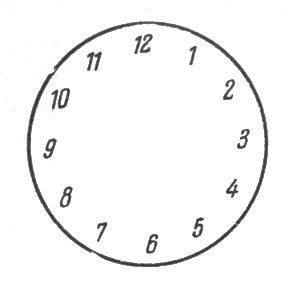
Рис. 93. Этот циферблат надо разрезать на 6 частей

Задача имеет целью испытать не столько вашу находчивость, сколько быстроту соображения.

122. Восьмиконечная звезда.

Числа от 1 до 16 надо расставить в точках пересечения линий фигуры, изображенной на рис. 94, так, чтобы сумма чисел на стороне каждого квадрата была 34, и сумма их на вершинах каждого квадрата также составляла 34.

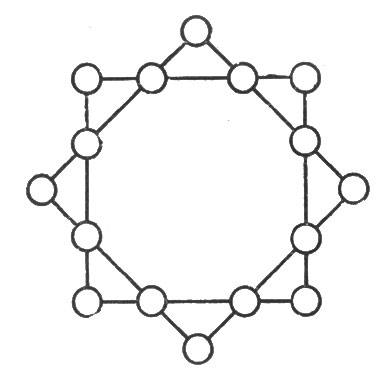
Рис. 94. Восьмиконечная звезда

123. Числовое колесо.

Цифры от 1 до 9 надо разместить в фигуре на рис. 95 так, чтобы одна цифра была в центре круга, прочие - у концов каждого диаметра, и чтобы сумма трех цифр каждого ряда составляла 15.

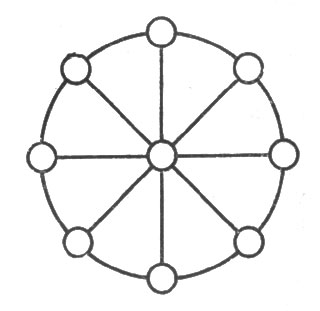
Рис. 95. Числовое колесо

124. Трехногий стол.

Существует мнение, что стол о трех ногах никогда не качается, даже если ножки его и неравной длины. Верно ли это?

125. Какие углы?

Какие углы составляют между собой стрелки часов на рис. 96? Ответ надо дать по соображению, не пользуясь транспортиром.

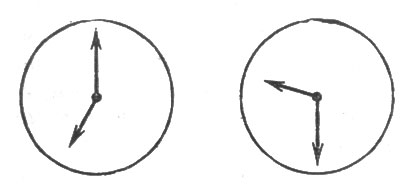
Рис. 96. Какой величины углы между стрелками?

126. По экватору.

Если бы мы могли обойти земной шар по экватору, то макушка нашей головы описала бы более длинный путь, чем каждая точка наших ступней. Как велика эта разница?

127. В шесть рядов.

Вам известен, вероятно, шуточный рассказ о том, как девять лошадей расставлены были по десяти стойлам и в каждом стойле оказалась одна лошадь. Задача, которая сейчас будет предложена, по внешности сходна с этой знаменитой шуткой, но имеет не воображаемое, а вполне реальное решение. Она состоит в следующем:

Расставить 24 человека в 6 рядов так, чтобы каждый ряд состоял из 5 человек.

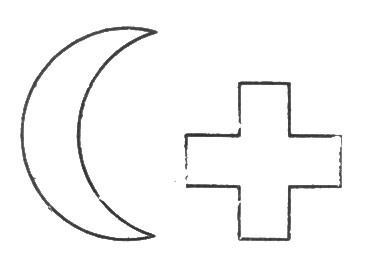
Рис. 97. Как 'превратить' полумесяц в крест

128. Крест и полумесяц.

На рис. 97 изображена фигура полумесяца (строго говоря, это не полумесяц, т. к. полумесяц имеет форму полукруга, а лунный серп), составленная двумя дугами окружностей. Требуется начертить знак Красного креста, площадь которого геометрически точно равнялась бы площади полумесяца.

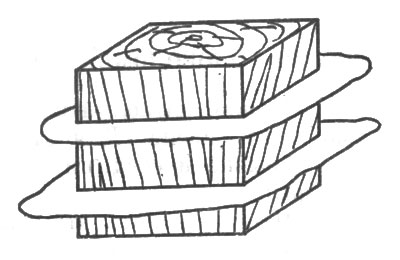
Рис. 98. Надо провести две плоскости, параллельные одной грани...

129. Разрез куба.

У вас имеется куб, ребро которого равно 3 см. Его объем равен 27 куб. см, и этот куб может быть разрезан на 27 маленьких кубиков, ребро каждого из которых равно 1см. Это очень легко сделать, разрезав куб шестью плоскостями: надо провести две плоскости, параллельные одной грани, две, параллельные другой грани, и две, параллельные третьей. Вообразите, однако, что после каждого разреза вам разрешено перемещать части в пространстве: отрезав какую-либо часть, вы можете наложить ее на другие так, чтобы следующая разрезающая плоскость пересекала их все. Не сможете ли вы, пользуясь этой дополнительной возможностью, уменьшить число разрезающих плоскостей, рассекающих куб на 27 маленьких кубиков?

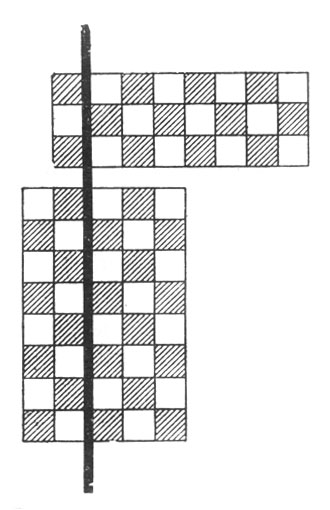
Рис. 99. Перед проведением очередного разреза образовавшиеся части можно перекладывать

130. Еще разрез.

Следующая задача похожа на предыдущую, но несколько в ином роде. Обычную шахматную доску, состоящую из 64 квадратиков (8 X 8), требуется разрезать на отдельные квадратики. При этом разрешается производить разрезы только по прямым линиям. Однако после каждого разреза можно перекладывать образовавшиеся части, чтобы следующий прямолинейный разрез мог рассечь не одну, а несколько частей. Сколько прямолинейных разрезов вам потребуется, чтобы разрезать всю доску на отдельные квадратики?