
Решения головоломок 72-94
72. На первый взгляд задача эта кажется не относящейся вовсе к геометрии. Но в том-то и состоит овладение этой наукой, чтобы уметь обнаруживать геометрическую основу задачи там, где она замаскирована посторонними подробностями. Наша задача по существу безусловно геометрическая; без знания геометрии ее не решить.
Итак, почему же передняя ось телеги стирается больше задней? Всем известно, что передние колеса меньше задних. На одном и том же расстоянии малый круг оборачивается большее число раз, чем круг покрупнее: у меньшего круга и окружность меньше - оттого она укладывается в данной длине большее число раз. Теперь понятно, что при всех поездках телеги передние ее колеса делают больше оборотов, нежели задние, а большее число оборотов, конечно, сильнее стирает ось.
73. Если вы полагаете, что в лупу угол наш окажется величиною в 1 1/2 X 4 = 6°, то дали промах. Величина угла нисколько не увеличивается при рассматривании его в лупу. Правда, длина дуги, стягивающей угол, несомненно увеличивается, - но во столько же раз увеличивается и радиус этой дуги, так что величина центрального угла остается без изменения. Рис. 77 поясняет сказанное.
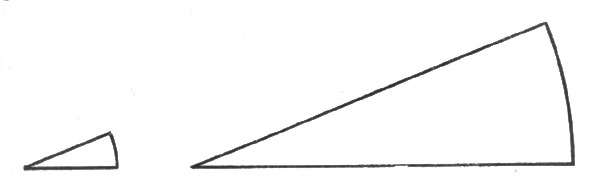
Рис. 77
74. Рассмотрите рис. 78, где MAN есть первоначальное положение дуги уровня, М'BN' - новое ее положение, причем хорда M'N' составляет с хордой MN угол в 1/2°. Оба положения уровня подобраны так, что пузырек, бывший раньше в точке А, теперь остался в той же точке, но середина дуги MN переместилась в В. Требуется вычислить длину дуги АВ, если радиус ее равен 1 м, а величина дуги в градусной мере 1/2° (это следует из равенства острых углов с перпендикулярными сторонами).
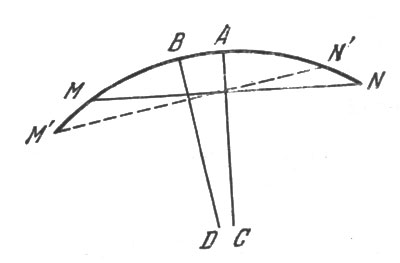
Рис. 78
Вычисление не сложно. Длина полной окружности радиусом в 1 м (1000 мм) равна 2 X 3,14 X 1000 = = 6280 мм. Так как в окружности 360° или 720 полуградусов, то длина одного полуградуса определяется делением
6280 : 720 = 8,7 мм.
Пузырек отодвинется от метки примерно на 9 мм - почти на целый сантиметр. Легко видеть, что чем больше радиус кривизны трубки, тем уровень чувствительнее.
75. Задача вовсе не шуточная и вскрывает ошибочность обычного словоупотребления. У "шестигранного" карандаша не 6 граней, как, вероятно, полагает большинство. Всех граней у него - если он не очинен - 8; шесть боковых и еще две маленькие "торцовые" грани. Будь у него в действительности 6 граней, он имел бы совсем иную форму - бруска с четырехугольным сечением.
Привычка считать у призм только боковые грани, забывая об основаниях, очень распространена. Многие говорят: трехгранная призма, четырехгранная призма и т. д., между тем как призмы эти надо называть: треугольная, четырехугольная и т. д. - по форме основания. Трехгранной призмы, т. е. призмы о трех гранях, даже и не существует.
Поэтому карандаш, о котором говорится в задаче, правильно называть не шестигранным, а шестиугольным.
76. Сделать надо так, как показано на рис. 79. Получаются 6 частей, которые для наглядности перенумерованы.
77. Спички следует расположить, как показано на рис. 80, а; площадь этой фигуры равна учетверенной площади "спичечного" квадрата. Как в этом удостовериться? Дополним мысленно нашу фигуру до треугольника. Получится прямоугольный треугольник, основание которого равно 3, а высота 4 спичкам*. Площадь его равна половине произведения основания на высоту: 1/2 X 3 Х 4 = 6 квадратам со стороною в одну спичку (рис. 80, б). Но наша фигура имеет, очевидно, площадь, которая меньше площади треугольника на 2 "спичечных" квадрата и равна, следовательно, 4 таким квадратам.
* (Читатели, знакомые с так называемой "Пифагоровой теоремой", поймут, почему мы с уверенностью можем утверждать, что получающийся здесь треугольник - прямоугольный: 32 + 42 = 52. )
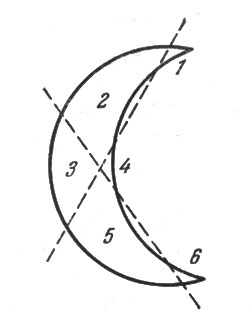
Рис. 79
78. Можно доказать, что среди всех фигур с контуром одной и той же длины (или, как говорят, с одинаковым периметром) наибольшую площадь имеет круг. Из спичек, конечно, не сложить круга; однако, можно составить из 8 спичек фигуру (рис. 81), всего более приближающуюся к кругу: это - правильный восьмиугольник. Правильный восьмиугольник и есть фигура, удовлетворяющая требованию нашей задачи: она имеет наибольшую площадь.
79. Для решения задачи развернем боковую поверхность цилиндрической банки в плоскую фигуру: получим прямоугольник (рис. 82), высота которого 20 см, а основание равно окружности банки, т. е. 10 X 3 1/7 = 31 1/2 см (без малого). Наметим на этом прямоугольнике положение мухи и медовой капли. Муха - в точке А, на расстоянии 17 см от основания; капля - в точке В, на той же высоте и в расстоянии полуокружности банки от А, т. е. в 153/4 см.
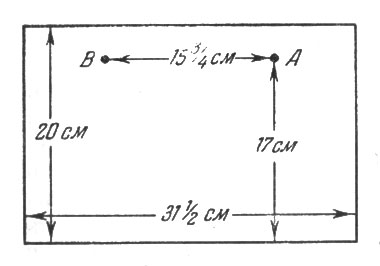
Рис. 82. Развернем боковую поверхность цилиндрической банки в плоскую фигуру: получим прямоугольник
Чтобы найти теперь точку, в которой муха должна переползти кран банки, поступим следующим образом. Из точки В (рис. 83) проведем прямую под прямым углом к верхней стороне прямоугольника и продолжим ее на равное расстояние: получим точку С. Эту точку соединим прямой линией с А. Точка D и будет та, где муха должна переползти на другую сторону банки, а путь ADB окажется самым коротким.
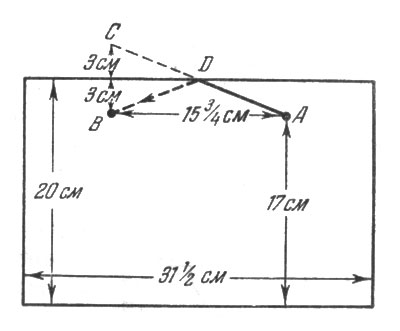
Рис. 83. Чтобы найти теперь точку, в которой муха должна переползти кран банки, поступим следующим образом
Найдя кратчайший путь на развернутом прямоугольнике, свернем его снова в цилиндр и узнаем, как должна бежать муха, чтобы скорее добраться до капли меда (рис. 84).
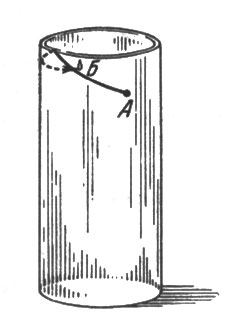
Рис. 84. Найдя кратчайший путь на развернутом прямоугольнике, свернем его снова в цилиндр и узнаем, как должна бежать муха, чтобы скорее добраться до капли меда
Избирают ли мухи в подобных случаях такой путь - мне не известно. Возможно, что, руководясь обонянием, муха действительно пробегает по кратчайшему пути, - но мало вероятно: обоняние для этого - недостаточно четкое чувство.
80. Нужная в данном случае затычка существует. Она имеет форму, показанную на рис. 85. Легко видеть, что одна такая затычка действительно может закрыть и квадратное, и треугольное, и круглое отверстия.
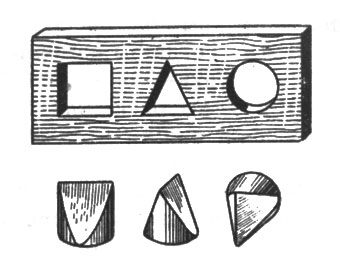
Рис. 85. Нужная в данном случае затычка существует
81. Существует затычка и для тех дыр, которые изображены на рис. 86: круглой, квадратной и крестообразной. Она представлена в трех положениях.
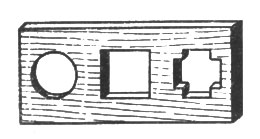
Рис. 86
82. Существует и такая затычка: вы можете видеть ее с трех сторон на рис. 87.
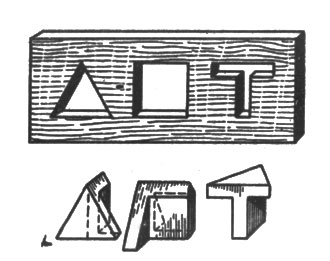
Рис. 87
(Задачи, которыми мы сейчас занимались, приходится нередко разрешать чертежникам, когда по трем "проекциям" какой-нибудь машинной части они должны установить ее форму.)
83. Как ни странно, но продеть пятак через такое маленькое отверстие вполне возможно. Надо только суметь взяться за это дело. Бумажку изгибают так, что круглое отверстие вытягивается в прямую щель (рис. 88): через эту щель и проходит пятак.
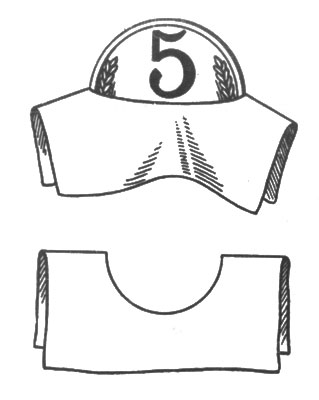
Рис. 88. Бумажку изгибают так, что круглое отверстие вытягивается в прямую щель
Геометрический расчет поможет понять этот на первый взгляд замысловатый трюк. Диаметр двухкопеечной монеты - 18 мм; окружность ее, как легко вычислить, равна 56 мм (с лишком). Длина прямой щели должна быть, очевидно, вдвое меньше окружности отверстия, и, следовательно, равна 28 мм. Между тем, поперечник пятака всего 25 мм; значит, он может пролезть через 28-миллиметровую щель, даже принимая в расчет его толщину (1 1/2 мм).
84. Чтобы по снимку определить высоту башни в натуре, нужно, прежде всего, измерить возможно точнее высоту башни и длину ее основания на фотографическом изображении. Предположим, высота на снимке 95 мм, а длина основания - 19 мм. Тогда вы измеряете длину основания башни в натуре; допустим, она оказалась равной 14 м.
Сделав это, вы рассуждаете так.
Фотография башни и ее подлинные очертания геометрически подобны друг другу. Следовательно, во сколько раз изображение высоты больше изображения основания, во столько же раз высота башни в натуре больше длины ее основания. Первое отношение равно 95 : 19, т. е. 5; отсюда заключаете, что высота башни больше длины ее основания в 5 раз и равна в натуре 14 X 5 = 70 м.
Итак, высота городской башни 70 м. Надо заметить, однако, что для фотографического определения высоты башни пригоден не всякий снимок, а только такой, в котором пропорции не искажены, как это бывает у неопытных фотографов.
85. Часто на оба поставленных в задаче вопроса отвечают утвердительно. В действительности же подобны только треугольники; наружный же и внутренний четырехугольники в фигуре рамки, вообще говоря, не подобны. Для подобия треугольников достаточно равенства углов; а так как стороны внутреннего треугольника параллельны сторонам наружного, то фигуры эти подобны Но для подобия прочих многоугольников недостаточно одного равенства углов (или - что то же самое - одной лишь параллельности сторон): необходимо еще, чтобы стороны многоугольников были пропорциональны. Для наружного и внутреннего четырехугольника в фигуре рамки это имеет место только в случае квадратов (и вообще - ромбов). Во всех же прочих случаях стороны наружного четырехугольника не пропорциональны сторонам внутреннего, и, следовательно, фигуры неподобны. Отсутствие подобия становится очевидным для прямоугольных рамок с широкими планками, как на рис. 89. В левой рамке наружные стороны относятся друг к другу, как 2:1, а внутренние - как 4:1. В правой - наружные, как 4:3, внутренние, как 2:1.
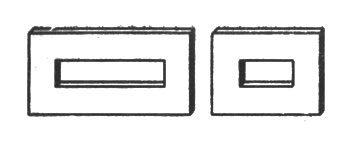
Рис. 89. Отсутствие подобия становится очевидным для прямоугольных рамок с широкими планками
86. Для многих будет неожиданностью, что при решении этой задачи понадобятся сведения из астрономии: о расстоянии Земли от Солнца и о величине солнечного диаметра.
Длина полной тени, отбрасываемой в пространстве проволокой, определяется геометрическим построением, показанными на рис. 90. Легко видеть, что тень во столько раз больше поперечника проволоки, во сколько раз расстояние Земли от Солнца (150000000 км) больше поперечника Солнца (1400000 км). Последнее отношение равно, круглым счетом, 115. Значит, длина полной тени, отбрасываемой в пространстве проволокой, равна
4 X 115 = 460 мм = 46 см.
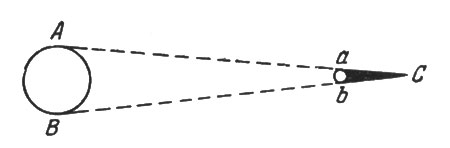
Рис. 90. Длина полной тени, отбрасываемой в пространстве проволокой, определяется геометрическим построением
Незначительной длиной полной тени объясняется то, что она бывает не видна на земле или на стенах домов; те слабые полоски, которые различаются при этом - не тени, а полутени.
Другой прием решения таких задач был указан при рассмотрении головоломки 8-й.
87. Ответ, что игрушечный кирпичик весит 1 кг, т. е. всего вчетверо меньше, грубо ошибочен. Кирпичик ведь не только вчетверо короче настоящего, но и вчетверо уже да еще вчетверо ниже, поэтому объем и вес его меньше в 4x4x4= 64 раза. Правильный ответ, следовательно, таков:
игрушечный кирпичик весит 4000 : 64 = 62,5 г.
88. Вы теперь уже подготовлены к правильному решению этой задачи. Так как фигуры человеческого тела приблизительно подобны, то при вдвое большем росте человек имеет объем не вдвое, а в 8 раз больший. Значит наш великан весит больше карлика раз в 8.
Самый высокий великан, о котором сохранились сведения, был один житель Эльзаса ростом в 275 см - на целый метр выше человека среднего роста. Самый маленький карлик имел в высоту меньше 40 см, т. е. был ниже исполина-эльзасца круглым счетом в 7 раз. Поэтому если бы на одну чашку весов поставить великана-эльзасца, то на другую надо бы для равновесия поместить 7 х 7 х 7 = 343 карлика - целую толпу.
89. Объем большого арбуза превышает объем меньшего в
1 1/4 х 1 1/4 х 1 1/4 = 125/64,
почти вдвое. Выгоднее, значит, купить крупный арбуз; он дороже только в полтора раза, а съедобного вещества в нем больше раза в два.
Почему же, однако, продавцы просят за такие арбузы обычно не вдвое, а только в полтора раза больше? Объясняется это просто тем, что продавцы в большинстве случаев не сильны в геометрии. Впрочем, не сильны в ней и покупатели, зачастую отказывающиеся из-за этого от выгодных покупок. Можно смело утверждать, что крупные арбузы выгоднее покупать, чем мелкие, потому что они расцениваются всегда ниже их истинной стоимости; но большинство покупателей об этом не подозревают.
По той же причине всегда выгоднее покупать крупные яйца, нежели мелкие, - если только их не расценивают по весу.
90. Окружности относятся между собой, как диаметры. Если окружность одной дыни 60 см, другой 50 см, то отношение их диаметров 60 : 50 = 6/5, а отношение их объемов
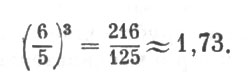
Большая дыня должна быть, если оценивать ее сообразно объему (или весу), в 1,73 раза дороже меньшей; другими словами, дороже на 73%. Просят же за нее всего на 50% больше. Ясно, что есть прямой расчет ее купить.
91. Из условия задачи следует, что диаметр вишни в 3 раза больше диаметра косточки. Значит, объем вишни больше объема косточки в 3 X 3 X 3, т. е. в 27 раз; на долю косточки приходится 1/27 объема вишни, а на долю сочной части - остальные 26/27. И, следовательно, сочная часть вишни больше косточки по объему в 26 раз.
92. Если модель легче натуры в 8000000 раз и обе сделаны из одного металла, то объем модели должен быть в 8000000 раз меньше объема натуры. Мы уже знаем, что объемы подобных тел относятся, как кубы их высот. Следовательно, модель должна быть ниже натуры в 200 раз, потому что
200 X 200 х 200 = 8000000.
Высота подлинной башни 300 м. Отсюда высота модели должна быть равна
300 : 200 = 1 1/2 м.
Модель будет почти в рост человека.
93. Обе кастрюли - тела, геометрически подобные. Если большая кастрюля в 8 раз вместительнее, то все ее линейные размеры в два раза больше: она вдвое выше и вдвое шире по обоим направлениям. Но раз она вдвое выше и шире, то поверхность ее больше в 2 X 2, т. е. в 4 раза, потому что поверхности подобных тел относятся, как квадраты линейных размеров. При одинаковой толщине стенок вес кастрюли зависит от величины ее поверхности. Отсюда имеем ответ на вопрос задачи: большая кастрюля вчетверо тяжелее меньшей.
94. Эта задача, на первый взгляд вовсе не математическая, решается в сущности тем же геометрическим рассуждением, какое применено было в предыдущей задаче.
Прежде чем приступить к ее решению, рассмотрим сходную с ней, но несколько более простую задачу.
Два котла (или два самовара), большой и малый, одинакового материала и формы наполнены кипятком. Какой остынет скорее?
Вещи остывают главным образом с поверхности: следовательно, остынет скорее тот котел, в котором на каждую единицу объема приходится большая поверхность. Если один котел в n раз выше и шире другого, то поверхность его больше в n2 раз, а объем - n3; на единицу поверхности в большом котле приходится в n раз больший объем. Следовательно, меньший котел должен остыть раньше.
По той же причине и ребенок, стоящий на морозе, должен зябнуть больше, чем одинаково одетый взрослый: количество тепла, возникающего в каждом куб. см тела, у обоих приблизительно одинаково, но остывающая поверхность тела, приходящаяся на каждый куб. см, у ребенка больше, чем у взрослого.
В этом нужно видеть также причину того, что пальцы рук или нос зябнут сильнее и отмораживаются чаще, чем другие части тела, поверхность которых не столь велика по сравнению с их объемом.
Сюда же, наконец, относится и следующая задача:
Почему лучина загорается скорее, чем толстое полено, от которого она отколота?
Так как нагревание происходит с поверхности и распространяется на весь объем тела, то следует сравнить поверхность и объем лучины (например, квадратного сечения) с поверхностью и объемом полена той же длины (и тоже квадратного сечения),, чтобы определить, какой величины поверхность приходится на каждый куб. см древесины в обоих случаях. Если толщина полена в 10 раз больше толщины лучины, то боковая поверхность полена больше поверхности лучины тоже в 10 раз, объем же его больше объема лучины в 100 раз. Следовательно, на каждую единицу поверхности в лучине приходится вдесятеро меньший объем, чем в полене: одинаковое количество тепла нагревает в лучине вдесятеро меньше вещества, - отсюда и более раннее воспламенение лучины, чем полена, от одного и того же источника тепла. (Ввиду дурной теплопроводности дерева указанные соотношения следует рассматривать лишь как грубо приблизительные; они характеризуют лишь общий ход процесса, а не количественную сторону.)
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'