10.06.2013

Джахит Арф - турецкий гений математики

Мы продолжаем серию публикаций о выдающихся мусульманских ученых современности. На этот раз речь пойдет о гениальном турецком математике Джахите Арфе (1910-1997). Имя этого человека звучит в названии теоремы, его портрет изображен на купюре в 10 новых турецких лир, а заслуги получили признание в научном мире...

В давние времена мусульманские ученые внесли поистине огромный вклад в развитие математических дисциплин. Многие термины, которые сейчас являются обыденными и всем понятными, произошли от арабских слов, использовавшихся в трудах ученых-мусульман той эпохи.

Однако после падения Аббасидского халифата, мусульманская прикладная наука постепенно начала приходить в упадок. И несмотря на то, что время от времени появлялись яркие ученые в среде мусульман, к концу XVI века положение было очень плачевным, - в плане развития науки мусульманский мир погрузился во мрак отсталости.

Некоторое возрождение стало наблюдаться со второй половины XIX столетия, со временем оно начало набирать обороты, хотя и нынешнее положение является далеким от удовлетворительного. Поэтому так важно освещать в мусульманской печати жизненный путь и достижения мусульманских ученых нашего времени, которые смогли добиться мирового признания и принести пользу человечеству своими трудами...

Джахит Арф смог достичь признания в математике - в области, которая является особо трудной для привнесения в нее чего-то нового. Основы и базовый инструментарий, главные представления этой науки уже давно не подвергались пересмотру, ибо их правильность доказана временем и опытом. Тем не менее, выдающемуся сыну турецкого народа, Джахиту Арфу, удалось внести свою лепту в развитие современной, особо сложной, математики, он смог совершить открытия в этой области...

Джахит Арф родился в городе Салоники 11 октября 1910 года. После Балканской войны 1912 года семья будущего ученого переехала в Измир, где Джахит получил начальное образование. После получения школьного образования он перебрался в Париж, где поступил в Высшую нормальную школу.

После возвращения в Турцию Арф преподавал математику в лицее Галатасарая. В 1933 году начал преподавать на кафедре математики Стамбульского университета.

В 1937 году уехал работать в Гёттингенский университет, где получил степень доктора философии, в дальнейшем стал работать с выдающимся математиком ХХ века Хельмутом Хассе, который стал его учителем и наставником.

Спустя некоторое время Арф вернулся в Турцию, снова работал в Стамбульском университете. В 1962 году он получил назначение в Совет по научно-техническим исследованиям (TUBITAK). В течении года Джахит Арф был председателем этого учреждения (ушел с должности в 1963 году).

В 1964-1966 годах работал в Принстонском университете, а затем, в течение года, в Калифорнийском университете в Беркли. После последнего возвращения в Турцию Арф был приглашен на кафедру математики Ближневосточного технического университета, где и работал до своей отставки в 1980 году. Последующие годы провел в Стамбуле, где и умер в 1997 году.

В математике имя Джахита Арфа связано с инвариантом Арфа квадратичной формы, применяемым в теории узлов в топологии, с группами и кольцами Арфа, а также с теоремой Хассе-Арфа, работами в области синтетической геометрии.

Ученый удостоился многих наград в сфере математики. Также трудно переоценить влияние Джахита Арфа на развитие турецкой математики. Хотя формально у него было мало учеников, многие турецкие математики сотрудничали с ним в начале своей карьеры и пользовались его доброжелательными советами.

Чтобы читатели смогли получить некоторое представление о сути работ турецкого математика, уместно объяснить, что такое инвариант Арфа.

Инвариант Арфа - инвариант квадратичной формы по модулю 2, заданной на целочисленной решетке, снабженной билинейной кососимметрич. формой. Пусть П - целочисленная решетка размерности k=2т и y(х, у) - форма, для которой y(х, y)=-y(y, х). Имеются базисы вида {е1, f1, . . ., е_т, f_m}, называемые симплектическими, в которых матрица формы y(х, у)приводится к блочнодиагональному виду: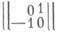 по диагонали стоят блоки, то есть y(e_i,f_i)=-y(f_i, e_i)=1, а в других местах - нули.

Пусть на П задано отображение 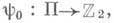, для которого y₀( х, y)=y₀(x)+y₀(y)+y(x, у)mod 2 - "квадратичная форма по модулю 2".

Выражение 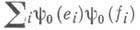и названо инвариантом Арфа. Если это выражение равно нулю, то существует симплектический базис, на всех элементах которого форма y₀ равна нулю, если же это выражение равно единице, то существует симплектический базис, на всех элементах которого, кроме е₁ и f₁, форма равна нулю, в то время как .

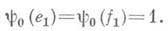Более подробно с вкладом Джахита Арфа в математику, с его достижениями, можно ознакомиться при прочтении статьи Масатоши Икеды «Вклад Джахита Арфа в алгебраическую теорию чисел и относительных полей».

Также следует отметить, что Джахит Арф был не просто выдающимся математиком, а и виртуозом в своем деле. Однажды он сказал: «Математика - это такое же искусство, как музыка, скульптура и рисование». Но при этом всегда повторял: «Для того, чтобы основательно овладеть математикой, необходимо терпение и упорство».

В заключение можно добавить, что в память о великом турецком математике, Джахите Арфе, ежегодно проводятся лекции математической кафедрой Ближневосточного Технического университета (Orta Dogu Teknik Universitesi), того самого, в котором ученый занимал последнюю должность в своей жизни. А открытия и достижения этого выдающегося человека всегда будут служить человечеству...

Юрий Косенко

Источники:

1. islam.com.ua