ЕГОРОВА ТЕОРЕМА

ЕГОРОВА ТЕОРЕМА о связи между понятиями сходимости почти всюду и равномерной сходимости последовательности функций: пусть μ есть σ-аддитивная мера, определенная на σ-алгебре Θ_μ, Е ∈Θ_μ и последовательность μ-измеримых почти везде конечных функций f_k(x), х∈Е, k=l, 2,..., сходится почти всюду к функции f(x); тогда для любого ε>0 существует такое измеримое множество Е_ε⊂ Е, что μ (Е\Е_ε)<ε, и на множестве Е_ε последовательность f_k(x) сходится к функции f(x) равномерно. В случае, когда μ — мера Лебега на прямой, это утверждение доказано Д. Ф. Егоровым [1].

Е. т. допускает различные обобщенные формулировки, расширяющие ее возможности. Пусть, напр., f_k(x) — последовательность измеримых отображений локально компактного пространства X в метризуемое пространство Y, причем предел

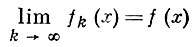
существует локально почти всюду на X по Радона мере μ≥0. Тогда функция f: X → Y измерима по мере μ и для любых компакта К⊂Х и числа ε>0 найдется компакт К₁⊂К такой, что μ(K∩K₁)<ε, а сужения f_k на К₁ непрерывны и равномерно сходятся на К₁ к f. Заключения Е. т. могут не выполняться, если Y не метризуемо.

Лит.: [1] Егоров Д. Ф., «С.г. Acad, sci», 1911, t. 152, p. 244—6; [2] Колмогоров A. H., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976.

Л. Д. Кудрявцев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.