ЕГОРОВА СИСТЕМА

ЕГОРОВА СИСТЕМА поверхностей — триортогональная система ∑, состоящая из потенциальных поверхностей; названа по имени Д. Ф. Егорова, подробно рассмотревшего (под названием потенциальных систем) в 1901 (см. [1]) общую теорию и многочисленные примеры систем указанного вида. Е. с. ∑ может быть определена как система, допускающая (однопараметрическую) группу преобразований, переводящих ∑ саму в себя таким образом, что нормали в соответственных точках ∑ остаются параллельными. Механическим истолкованием этой группы служит переносящее поверхности Е. с. стационарное течение жидкости, имеющее потенциал скоростей.

Пусть

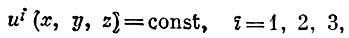
— уравнения поверхностей, образующих Е. с. ∑, H_i — коэффициенты Ламе, фигурирующие в выражении квадрата линейного элемента пространства в криволинейных координатах {uⁱ}:

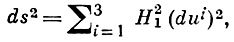
P_i — расстояние начала координат от трех касательных плоскостей ∑, R_ik — главные радиусы кривизны поверхности uⁱ = const, соответствующие элементу дуги H_kdu^k, β_ik= —H_k/R_ik — величины, через к-рые выражаются линейные элементы dσ_i сферич. изображений поверхностей:

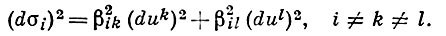
Функции Р_i и H_i удовлетворяют одной и той же системе уравнений:

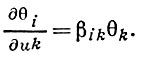
Решения этих уравнений определяют еще две Е. с. ∑₁ и ∑_-1 того же сферич. изображения, для к-рых

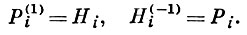
Продолжение этого преобразования в ту и другую стороны дает ряд Е. с. (ряд Егорова)

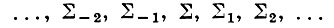
одного сферич. изображения, из к-рых каждая следующая ∑_k+1 получается из предыдущей ∑_k с помощью формул:

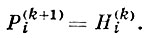
И вообще, изыскание сферич. изображения Е. с. ∑ приводится к изысканию потенциальной системы на сфере: любую такую систему можно принять за сферич. изображение одного из трех семейств, составляющих ∑.

Е. с. ∑ характеризуется тем, что

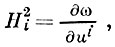
где ω — некоторая функция, имеющая смысл потенциала скоростей соответствующего течения, т. е. uⁱ = const — потенциальные поверхности. При этом, для любой потенциальной поверхности S определяется Е. с. ∑, в состав к-рой входит S. Касательная к линии пересечения какой-либо поверхности ω = const с поверхностью uⁱ = const в любой точке параллельна лучу lⁱ, соединяющему центры геодезич. кривизн линий кривизны поверхности uⁱ = const; во всякой точке пространства три луча l¹, l², l³ параллельны одной и той же плоскости — касательной плоскости поверхности ω = const, а соприкасающиеся плоскости координатных линий проходят через одну прямую. Величины β_ik и R_ik для Е. с. удовлетворяют соотношениям:

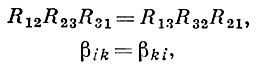
(симметричность β_ik также необходима и достаточна для того, чтобы триортогональная система была Е. е.).

Лит.: [1] Егоров Д. Ф., Работы по дифференциальной геометрии, М., 1970.

М. И. Войцеховский.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.