ЕВКЛИДОВО КОЛЬЦО

ЕВКЛИДОВО КОЛЬЦО — область целостности с единицей такая, что всякому ее элементу а, отличному от нуля, поставлено в соответствие неотрицательное целое число n(а), причем выполняется следующее требование: для любых двух элементов а, b, если b≠0, можно так подобрать элементы q и г, что

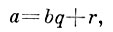
причем или r = 0, или n(r) < n(b).

Всякое Е. к. является главных идеалов кольцом и, следовательно, факториальным кольцом, однако, существуют кольца главных идеалов, не являющиеся евклидовыми. К числу Е. к. принадлежат кольцо целых чисел (роль n(а) в нем играет абсолютная величина |а|), а также кольцо многочленов от одного переменного над полем (n(а) — степень многочлена). Во всяком Е. к. для разыскания наибольшего общего делителя двух элементов можно применять Евклида алгоритм.

Лит.: [1] Курош А. Г., Лекции по общей алгебре, 2 изд., М., 1973.

О. А. Иванова.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.