ДЮАМЕЛЯ ИНТЕГРАЛ

ДЮАМЕЛЯ ИНТЕГРАЛ - представление решения Коши задачи или смешанной задачи с однородными граничными условиями для неоднородного линейного уравнения с частными производными через решение соответствующей задачи для однородного уравнения. Пусть для уравнения

∂²u(t, x)/∂t² + L[u(t, x)] = f(t, x); t > 0, x ∈ R_n, (1)

где L - линейный дифференциальный оператор с независящими от t коэффициентами, содержащий производные по t не выше 1-го порядка, поставлена задача Коши с начальными условиями:

u(t, x)|_t=0 = 0, ∂u(t, x)/∂t|_t=0 = 0 (2)

И пусть достаточно гладкая функция v(t, х; τ), t ≥ τ, τ ≥ 0, х ∈ R_n является при t > τ решением однородного уравнения

∂²v(t, x, τ)/∂² + L[v(t, x; τ)] = 0,

удовлетворяющим при t = τ начальным условиям:

v(t, x, τ)|_t=τ = 0, ∂v(t, x, τ)/∂t|_t=τ = f(τ, x).

Тогда решение задачи Коши (1), (2) выражается Д. и.:

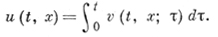
Сформулированное утверждение носит название принципа Дюамеля и является аналогом метода вариации постоянных.

Аналогичное построение можно провести и в случае задачи Коши с однородным начальным условием для уравнения

∂u(t, x)/∂t = f(t, х); t > 0; x ∈ R_n,

где М - линейный дифференциальный оператор с независящими от t коэффициентами, содержащий производные только по переменным х.

Решение задачи Коши с однородными начальными условиями для неоднородного уравнения теплопроводности выражается Д. и.

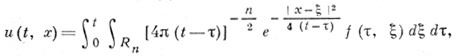
а для волнового уравнения в случае n = 1

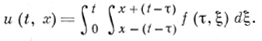
Д. и. наз. по имени Ж. Дюамеля (J. Duhamel).

Лит.: [1] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966; [2] Йон Ф., Плоские волны И сферические средние в применении к дифференциальным уравнениям с частными производными, пер. с англ., М., 1958.

А. К. Гущин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.