ДРОБНЫХ ШАГОВ МЕТОД

ДРОБНЫХ ШАГОВ МЕТОД - метод построения экономичных (в смысле числа операций) устойчивых разностных схем для решения дифференциальных уравнений математич. физики.

При увеличении размерности задачи число операций для получения численного решения растет как вследствие роста числа точек, так и вследствие логич. трудностей составления программы расчета. Для системы дифференциальных уравнений

∂u/∂t = Lu, (1)

где L = L(∂/∂x) - дифференциальный оператор, u = u(х, t), х = (x₁, ..., х_n), абсолютно устойчивые неявные схемы простой аппроксимации

(uⁿ⁺¹ - uⁿ)/τ = Λ₁uⁿ⁺¹ + Λuⁿ, (2)

Λ₀ ~ L₀, Λ₁ ~ L₂, L₀ + L₁ = L,

становятся неэффективными в случае многомерных задач. В одних случаях требуется использовать слишком мелкий шаг по времени, в других нахождение каждого uⁿ⁺¹ требует const ⋅ N^α(m) операций, где N- число точек на одно измерение, m - число пространственных измерений, а α(m) сильно растет с увеличением m.

Для получения экономичных устойчивых разностных схем предложены методы, основанные на следующих идеях:

1) расщепления разностных схем;

2) приближенной факторизации;

3) расщепления (слабой аппроксимации) дифференциальных уравнений.

В случае уравнения (1) соответствующие разностные схемы имеют вид (для простоты взяты два дробных шага и рассматривается периодич. задача Коши):

схема расщепления:

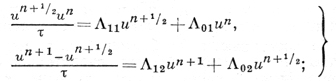
(3)

схема приближенной факторизации:

(E - τΛ₁₁)(E - τΛ₁₂)uⁿ⁺¹ = (E + τΩ)uⁿ, (4)

Λ₁₁ + Λ₁₂ = Λ₁, Ω ~ Λ₀

схема слабой аппроксимации:

∂u/∂t = (α₁L₁ + α₂L₂)u = Lu, L = L₀ + L₁, (5)

α₁(t, τ) = 2, α₂(t, τ) = 0 при t ∈ [nτ, (n + 1/2)τ],

α₁(t, τ) = 0, α₂(t, τ) = 2 при t ∈ [(n + 1/2)τ, (n + 1)τ].

В случае схем (3) и (4) обращение оператора Е - τΛ₁ заменяется обращением оператора (Е - τΛ₁₁)(E - τΛ₁₂), т. е. последовательным обращением операторов Е - τΛ₁₁, Е - τΛ₁₂, вообще говоря, более простой структуры.

Трактовка (5) позволяет рассматривать схему расщепления

(u^n+1/2 - uⁿ)/τ = Λ₁u^n+1/2, (uⁿ⁺¹ - u^n+1/2)/τ = Λ₂uⁿ⁺¹

как простую аппроксимацию уравнения (5), слабо аппроксимирующего уравнение (1).

Таким образом, в основе этих методов лежит представление сложных операторов через простейшие, при этом интегрирование исходного уравнения сводится к интегрированию уравнений более простой структуры, а методы дробных шагов обязаны удовлетворять условиям аппроксимации и устойчивости только в окончательном итоге (при записи их в «целых» шагах). Методом расщепления решаются многие сложные задачи математич. физики.

Большое развитие получили схемы расщепления повышенного порядка точности. К одной из модификаций метода расщепления принадлежит метод «частиц в ячейках»: здесь расщепление производится по физическим процессам и не связано с понижением размерности операторов.

Лит.: [1] Яненко Н. Н., Метод дробных шагов решения многомерных задач математической физики, Новосиб., 1967; [2] Самарский А. А., Введение в теорию разностных схем, М., 1971.

Н. Н. Яненко.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.