ДРОБНО-ЛИНЕЙНОЕ ОТОБРАЖЕНИЕ

ДРОБНО-ЛИНЕЙНОЕ ОТОБРАЖЕНИЕ, дробно-линейное преобразование,- отображение комплексного пространства ℂⁿ → ℂⁿ, осуществляемое дробно-линейными функциями.

В случае комплексной плоскости ℂ¹ = ℂ - это отличное от константы отображение вида

z → w = L(z) = (az + b)/(cz + d), (1)

где ad - bс ≠ 0; часто применяется унимодулярная нормировка ad - bс = 1. Всякое Д.-л. о. доопределяется соответствиями ∞ → а/с и -d/c → ∞ до взаимно однозначного отображения расширенной плоскости ℂ на себя. Простейшими среди Д.-л. о. являются линейные: z → w = ãz + b̃, получающиеся при с = 0. Всякое нелинейное Д.-л. о. представимо в виде суперпозиции двух линейных отображений и отображения L₀: z → w = 1/z. Свойства Д.-л. о. L₀ становятся наглядными на Римана сфере, так как при стереографич. проекции ему соответствует поворот сферы на 180^○ вокруг диаметра, проходящего через образы точек ±1 ∈ ℂ.

Основные свойства. Д--л. о. отображает взаимно однозначно и конформно ℂ̅ на себя. Круговое свойство: при Д.-л. о. любая окружность на ℂ̅ (т. е. окружность на ℂ или прямая, пополненная точкой ∞) переходит в окружность на ℂ̅. Инвариантность отношения симметрии двух точек: пара точек z, z*, симметричных относительно какой-либо окружности на ℂ̅, при Д.-л. о. переходит в пару точек w, w*, симметричных относительно образа этой окружности. Двойное отношение четырех точек на ℂ̅ инвариантно относительно Д.-л. о., т. е. если точки ξ₁, ξ₂, ξ₃, ξ₄ при Д.-л. о. переходят соответственно в ζ₁, ζ₂, ζ₃, ζ₄, то

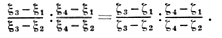
Для любых заданных троек ξ₁, ξ₂, ξ₃ и ζ₁, ζ₂, ζ₃, попарно различных точек на ℂ̅, существует и притом только одно Д.-л. о., переводящее соответственно ξ_k → ζ_k, k = 1, 2, 3.

Это Д.-л. о. можно найти из уравнения (2), подставляя в него z и w соответственно вместо ξ₄ и ζ₄. Групповое свойство: совокупность всех Д.-л. о. образует некоммутативную группу относительно суперпозиции (L₁L₂)(z) = L₁(L₂(z)) с единицей E(z) = z. Свойство универсальности: всякий конформный автоморфизм ℂ̅ есть Д.-л. о., и, таким образом, группа всех Д.-л. о. совпадает с группой Aut ℂ̅ всех конформных автоморфизмов ℂ̅.

Все конформные автоморфизмы единичного круга B = {z ∈ ℂ; |z| < 1} образуют подгруппу Aut В группы Aut ℂ̅, состоящую из Д.-л. о. вида:

Так же обстоит дело с конформными автоморфизмами верхней полуплоскости {z ∈ ℂ; Im z > 0}, имеющими вид:

z → w = (az + b)/(cz + d), Im(а, b, с, d) = 0, ad - bc > 0.

Все конформные гомеоморфизмы верхней полуплоскости на единичный круг имеют вид:

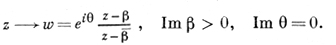
Исключив тождественное Д.-л. о. E(z), можно сказать, что Д.-л. о. имеет не более двух различных неподвижных точек ξ₁, ξ₂ на ℂ̅. В случае двух различных неподвижных точек ξ₁ ≠ ξ₂ семейство окружностей Σ, проходящих через ξ₁ и ξ₂, переводится Д.-л. о. (1) само в себя. При этом семейство Σ' всех окружностей, ортогональных к окружностям 2, также переходит само в себя. Здесь возможны в свою очередь три случая.

1) Каждая окружность Σ переходит сама в себя; такое Д.-л. о. наз. гиперболическим, и оно представимо в нормальной форме:

(w - ξ₁)/(w - ξ₂) = μ(z - ξ₁)/(z - ξ₂), (3)

где множитель Д.-л. о. ⍠ > 0, |μ| ≠ 1, ∞. Унимодулярное Д.-л. о. (1) является гиперболическим тогда и только тогда, когда a + d ∈ ℝ и |a + d| > 2.

2) Каждая окружность Σ' переходит сама в себя; такое Д.-л. о. наз. эллиптическим и в нормальной форме (3) характеризуется множителем μ таким, что |μ| = 1, μ ≠ 1. Унимодулярное Д.-л. о. (1) является эллиптическим тогда и только тогда, когда a + d ∈ ℝ, |a + d| < 2.

3) Ни одна из окружностей семейств Σ и Σ' не переходит сама в себя; такое Д.-л. о. называется локсодромическим и в нормальной форме (3) характеризуется множителем μ ∈ ℂ, |μ| ≠ 1, таким, что либо Im μ ≠ 0, либо μ < 0. Унимодулярное Д.-л. о. (1) является локсодромическим тогда и только тогда, когда a + d ∈ ℂ\ℝ

Если же две неподвижные точки сливаются в одну ξ₁, то Д.-л. о. наз. параболическим. Семейство Σ состоит при этом из всех окружностей, имеющих в ξ₁ общую касательную; каждая окружность Σ переходит сама в себя. Нормальная форма параболич. Д.-л. о. имеет вид либо

1/(w - ξ₁) = 1/(z - ξ₁) + α, α ∈ ℂ, α ≠ 0,

при ξ₁ #&8800; ∞, либо

w = z + α, α ∈ ℂ, α ≠ 0,

при ξ₁ = ∞. Унимодулярное Д.-л. о. (1) является параболическим тогда и только тогда, когда a + d = ±2.

Благодаря перечисленным богатым элементарным свойствам, Д.-л. о. находят самое широкое применение во всех разделах теории функций комплексного переменного и в различных прикладных дисциплинах. В частности, Д.-л. о. позволяют построить модель Лобачевского геометрии.

Среди подгрупп общей группы всех Д.-л. о. наиболее важны, с точки зрения их применений для аналитич. теории дифференциальных уравнений, теории автоморфных функций и других вопросов анализа, дискретные группы Г Д.-л. о. Элементарные дискретные группы Д.-л. о.- это конечные группы; они изоморфны либо циклическим группам вращений сферы Римана, либо группам вращений правильных многогранников. Дискретные группы Д.-л. о. Г, имеющие инвариантную окружность γ на ℂ̅, общую для всех преобразований Г, причем внутренность γ при всех преобразованиях Г переходит сама в себя, наз. фуксовыми группами. Локсодромич. Д.-л. о. не может быть фуксовым. Исторически первым примером фуксовой группы была Moдyлярная группа, возникшая в теории эллиптич. функций (см. также Moдyляpнaя функция). Модулярная группа состоит из всех унимодулярных Д.-л. о. (1), у к-рых коэффициенты а, b, с, d - целые действительные числа; действительная ось инвариантна относительно модулярных Д.-л. о. Более сложны и менее изучены неэлементарные группы Д.-л. о., не являющиеся фуксовыми,- клейновы группы.

Д.-л. о. комплексного пространства ℂⁿ, n ≥ 1, наз. невырожденное отображение

z = (z₁, ..., z_n) → w = (w₁, ..., w_n) = (L₁(z), ...,L_n(z)),

осуществляемое дробно-линейными функциями

L_k(z) = (a_1kz₁ + ... + a_nkz_n + b_k)/(c_1kz₁ + ... + c_nkz_n + d_k), k = 1, ..., n.

Наиболее важны те Д.-л. о. ℂⁿ, к-рые продолжаются в какую-либо компактификацию ℂⁿ. Так, в пространство теории функций ℂ̅ⁿ продолжаются все линейные преобразования, переставляющие координаты, а также Д.-л. о. вида

z = (z₁, ..., z_n) → w = (L₁(z₁), ..., L_n(z_n)),

где L_k(z_k) - Д.- л. о. вида (1) на плоскости z_k. Порождаемая перечисленными отображениями группа Д.-л. о. совпадает с группой Aut ℂ̅ⁿ всех биголоморфных автоморфизмов компактификации ℂ̅ⁿ. Соответствующая подгруппа Aut Uⁿ с

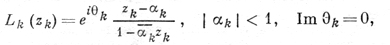
исчерпывает все автоморфизмы единичного поликруга Uⁿ = {z ∈ ℂⁿ; |z_j| < 1, j = 1, ..., n). В проективное замыкание ℂРⁿ пространства ℂⁿ продолжаются Д.-л. о., у к-рых

L_k(z) = (a_1kz₁ + ... + a_nkz_n + b_k)/(c₁z₁ + ... + c_nz_n + d) = l_k(z)/l(z),

в однородных координатах это продолжение имеет вид

(z₀, z₁, ..., z_n) → (z₀l(z/z₀) , z₀l₁(z/z₀), ..., z₀l_n(z/z₀))).

Этими отображениями исчерпывается группа Aut ℂPⁿ всех биголоморфных автоморфизмов ℂРⁿ. Автоморфизмы единичного шара Вⁿ = {z ∈ ℂⁿ; |z| < 1} образуют подгруппу Aut Bⁿ группы Aut ℂPⁿ, состоящую из всех Д.-л. о. вида (4), у к-рых коэффициенты подчинены известным дополнительным условиям (см. [2], ч. 2).

Лит.: [1] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [2] Шабат Б. В., Введение в комплексный анализ, 2 изд., ч. 1-2, М., 1976; [3] Стойлов С., Теория функций комплексного переменного, пер. с рум., т. 1, М., 1962; [4] Форд Л. Р., Автоморфные функции, пер. с англ., М.- Л., 1936.

Е. П. Долженко, Е. Д. Соломенцев, Е. М. Чирка.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.