ДРОБНОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ

ДРОБНОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ - распространение операций интегрирования и дифференцирования на случай дробных порядков.

Пусть f(x) интегрируема на отрезке [a, b], I^a₁f(x) -интеграл от f по [а, х], a I^a_αf(x) - интеграл от I^a_α-1f(x) по [а, х], α = 2, 3, ... . Имеет место соотношение

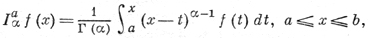
(1)

где Г(α) = (α - 1)! - гамма-функция. Правая часть в (1) имеет смысл при всех α > 0. Соотношение (1) определяет дробный интеграл (или интеграл Римана - Лиувилля) порядка α от f с началом в точке а. Оператор I^a_z при комплексных значениях параметра z изучался Б. Риманом (В. Riemann, 1847). Оператор I^a_α линеен и обладает полугрупповым свойством:

I^a_α[I^a_βf(x)] = I^a_α+βf(x).

операция, обратная дробному интегрированию, носит название дробного дифференцирования: если I_αf = F, то f есть дробная производная порядка α от F. При 0 < α < 1 имеет место формула Маршо:

Понятие Д. и. и д. впервые ввел Ж. Лиувилль (J. Liouville, 1832), в частности он рассмотрел оператор I^∞_α = I_α, α > 0:

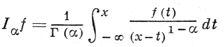
(при соответствующих ограничениях на функцию f; см. [1], где приведены также оценки оператора I_α в L_p).

Для интегрируемой 2π-периодической функции f(x) с нулевым средним значением по периоду удобно (см. [2]) определение, предложенное Г. Вейлем (Н. Weyl, 1917): если

f(x) ~ ∑_|n|>0 c_ne^inx = ∑' c_ne^inx,

то интеграл Вейля f_α(х) порядка α > 0 функции f определяется формулой

f_α(x) ~ ∑' c_ne^inx/(in)^α; (2)

производная f^β порядка β > 0 определяется при этом равенством

f^β(x) = dⁿ/dxⁿ f_n-β(x),

где n - наименьшее целое, большее β (отметим, что f_α(x) совпадает с I_αf(x)).

Перечисленные определения получили дальнейшее развитие в рамках теории обобщенных функций. Для периодических обобщенных функций

f ~ ∑' c_ne^inx

операция дробного интегрирования I_αf = f_α выполнима по формуле (2) для любых действительных α (при отрицательных α I_αf совпадает с дробной производной порядка α) и обладает групповым свойством по параметру α.

В n-мерном пространстве X аналогом оператора дробного интегрирования является риссов потенциал (или интеграл типа потенциала)

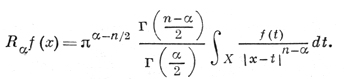
Обратная к R_α операция наз. риссовой производной порядка α.

Лит.: [1] Xарди Г. Г., Литтльвуд Д. Е., Полна Г., Неравенства, пер. с англ., М., 1948; [2] Зигмунд А., Тригонометрические ряды, пер. с англ., т. 1, М., 1965; [3] Xилле Э., Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., 2 изд., М., 1962; [4] Джрбашян М. М., Интегральные преобразования и представления функций в комплексной области, М., 1966.

П. И. Лизоркин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.