ДРОБНАЯ СТЕПЕНЬ

ДРОБНАЯ СТЕПЕНЬ линейного оператора А в комплексном банаховом пространстве Е - функция f(A) от этого оператора такая, что f(z) = z^α. Если оператор А ограничен, и спектр его не содержит и не окружает нуля, то А^α определяется Коши интегралом по контуру, окружающему спектр А и не содержащему внутри себя нуль. Если А неограничен, то контур приходится брать бесконечным, и возникают вопросы об условиях сходимости интеграла. Если А имеет плотную в Е область определения D(А) и при λ < 0 имеет резольвенту R(λ, А) = (А - λI)^-1

с оценкой

||R(-s, A)|| ≤ M(1 + s)^-1, s > 0, (1)

то

A^-α = 1/2πi ∫_Г λ^α R(λ, A) dλ,

где Г состоит из сторон угла, строящегося по М. Операторы А^-α ограничены и А^-αх → х при любом х ∈ Е и α → 0. Положительные степени определяются так: А^α = (А^-α)^-1; они уже являются неограниченными. При любых действительных α и β выполнено основное свойство степеней

A^αA^βx = A^βA^αx = A^α+βx

для x ∈ D(A^γ) и γ = mах{α, β, α + β}. При 0 < α < 1 (A^α)^β = A^αβ. При любых α < β < γ и x ∈ D(A^γ)

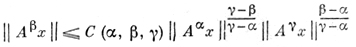
(неравенство моментов). Полугруппа степеней А^-α допускает расширение до полугруппы A^-z, аналитической в правой полуплоскости.

Ряд приведенных свойств Д. с. обобщается на случай, когда А не имеет ограниченного обратного и справедлива оценка ||R(-s, A)|| ≤ Ms^-1, s > 0. При условии (1) и при 0 < α < 1

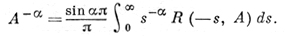
Если оператор В - производящий оператор сжимающей полугруппы U(t), то

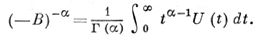
Из условия (1) не вытекает, что -А является производящим оператором сильно непрерывной полугруппы, но оператор -А^α при α ≤ 1/2 является производящим оператором аналитич. полугруппы.

Оператор В подчинен оператору А, если D(B) ⊃ D(A) и ||Bx|| ≤ с||Ax||, x ∈ D(A). Если В подчинен А и резольвенты обоих операторов обладают свойством (1), то В^α подчинен A^β при 0 ≤ α < β ≤ 1.

Если А - положительный самосопряженный оператор в гильбертовом пространстве, то его Д. с. определяется через спектральное разложение

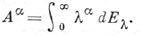
В неравенстве моментов для такого оператора константа с(α, β, γ) = 1. Пусть А и В - два самосопряженных положительных оператора, действующие в гильбертовых пространствах Н и Н₁ соответственно. Если Т - такой ограниченный линейный оператор из Н в Н₁ с нормой М, что TD(A) ⊂ D (В) и ||ВТх|| ≤ М₁||Ax||, x ∈ D(A), то TD(A^α) ⊂ D(В^α) и

||В^αТх|| ≤ M^1-α M^α₁||A^αх||, 0 ≤ α ≤ 1

(неравенство Хайнца). В частности, при Н = Н₁ и Т = I из подчиненности В оператору А следует подчиненность В^α оператору А^α при 0 ≤ α ≤ 1. Д. с. операторов применяются при исследовании нелинейных уравнений. Они детально изучены для операторов, порожденных эллиптич. праевыми задачами.

Лит.: [1] Функциональный анализ. [Справочная математическая библиотека], 2 изд., М., 1972; [2] Крейн С. Г., Линейные дифференциальные уравнения в банаховом пространстве, М., 1967; [3] Сили Р., «Математика», 1968, т. 12, № 1, с. 96 - 112.

С. Г. Нрейн.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.