ДРЕВОВИДНОЕ МНОГООБРАЗИЕ

ДРЕВОВИДНОЕ МНОГООБРАЗИЕ - гладкое нечетномерное многообразие специального вида, являющееся краем четномерного многообразия, строящегося из расслоений над сферами с помощью склеек по схеме, задаваемой нек-рым графом (деревом).

Пусть p_i: E²ⁿ_i → Sⁿ_i, i = 1, 2, ... - расслоение над n-сферами со слоем n-шар Dⁿ и структурной группой SO_n и пусть Вⁿ_i - замкнутый стандартный n-шар в n-сфере Sⁿ_i; тогда

P^-1_i(Bⁿ_i) ≈ Bⁿ_i × Dⁿ_i

где Dⁿ_i - слой расслоения р_i. Пусть

γ_ij: Bⁿ_i × Dⁿ_i → Bⁿ_j × Dⁿ_j, i = 1, 2,

- гомеоморфизм, осуществляющий склейку двух расслоений p_i, p_j и переводящий каждый n-шар Вⁿ × х из Bⁿ_i × Dⁿ_i в некоторый шар y × Dⁿ из Bⁿ_j × Dⁿ_j (склейка меняет сомножители прямого произведения Bⁿ × Dⁿ). Результатом склейки двух расслоений р_i, p_j является 2n-мерное многообразие E²ⁿ_i ∪_γijE²ⁿ_j, к-рое превращается в гладкое многообразие с помощью операции «сглаживания углов».

Расслоения Е²ⁿ_i рассматриваются как «строительные блоки», из к-рых с помощью попарных склеек результирующее гладкое многообразие строится следующим образом. Пусть Т - одномерный конечный комплекс (граф). Каждой вершине графа Т сопоставляется блок E²ⁿ_i, выбираются в Sⁿ_i непересекающиеся n-шары Bⁿ_ik в количестве k = 1, 2, ..., равном индексу ветвления соответствующей вершины, и производится склейка по схеме, указанной графом Т. Полученное таким образом многообразие с краем обозначается (опуская зависимость от выбора расслоений Е²ⁿ_i) через W²ⁿ(T). В случае, если Т есть дерево, то есть граф без циклов, то край ∂W²ⁿ(Т) = М^2n-1 наз. древовидным многообразием.

Если Т - дерево, то W²ⁿ(T) имеет гомотопич. тип букета n-сфер в количестве, равным числу вершин дерева Т.

Д. м. M^2n-1 = ∂W²ⁿ(T) является целочисленной гомологии. (2n - 1)-сферой тогда и только тогда, когда определитель матрицы целочисленной билинейной (-1)ⁿ-формы пересечений, определенной на решетке n-мерных гомологии H_n(W²ⁿ, ℤ), равен ±1. Если это условие выполнено, то многообразие W²ⁿ(T) наз. плюмбингом.

Если Т - произвольный граф и n ≥ 2, то W²ⁿ(T) тогда и только тогда односвязно, когда Т - дерево. Если Т - дерево и n ≥ 3, то ∂W²ⁿ(T) односвязно; если W²ⁿ - плюмбинг, то край ∂W²ⁿ является гомотопич. сферой, n ≥ 3.

Если плюмбинг W^4k - параллелизуем, то на главной диагонали матрицы пересечений 2k-мерных циклов стоят четные числа; в этом случае сигнатура матрицы пересечений делится на 8. Плюмбинг W^4k тогда и только тогда параллелизуем, когда все расслоения над S^2k, использованные при построении W^4k, являются стабильно тривиальными; напр., если все расслоения, используемые при построении W^4k, являются касательными расслоениями на диски над 2k-мерными сферами, то плюмбинг W^4k параллелизуем. Плюмбинг W^4k+2 тогда и только тогда параллелизуем, когда каждое расслоение Е^4k+2_i, используемое в качестве блоков при построении плюмбинга W^4k+2, принадлежит к одному из двух типов: оно либо тривиально, либо является трубчатой окрестностью диагонали в произведении S^2k+1 × S^2k+1, то есть касательным расслоением на диски над S^2k+1. Если плюмбинг W^4k+2 параллелизуем, то его матрица пересечений приводится к симплектическому виду, состоящему из блоков 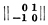, расположенных вдоль главной диагонали.

Среди плюмбингов особо выделяются многообразия Милнора размерности 4k, k > 1 и многообразия Кервера размерности 4k + 2, k ≥ 0. Многообразия Милнора строятся следующим образом: в качестве блоков берутся несколько экземпляров трубчатой окрестности E^4k диагонали в произведении S^2k × S^2k; в качестве графа Т берется граф следующего вида:

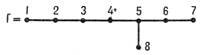
При этих условиях многообразие W^4k(Г) реализует

квадратичную форму 8-го порядка, у которой на главной диагонали стоят двойки, а сигнатура равна 8.

Для построения многообразий Кервера K^4k+2 берутся два экземпляра блока, получающегося как трубчатая окрестность E^4k+2 диагонали в произведении S^2k+1 × S^2k+1. Склеиваются они так, что матрица пересечений имеет вид .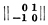

Край многообразия Милнора ∂М^4k (сферы Милнора) всегда недиффеоморфен стандартной сфере S^4k-1 относительно многообразий Кервера этот вопрос до конца не решен (1978). Если 2k + 1 ≠ 2ⁱ - 1, то край многообразия Кервера ∂K^4k+2 (сферы Кервера) всегда нетривиален, если же 2k + 1 = 2ⁱ - 1, то для 1 ≤ i ≤ b получится стандартная сфера S^4k+1,

для остальных i решение неизвестно (см. Кервера инвариант).

Многообразия Кервера К^4k+2 размерности 2, 6, 14 представляют собой произведения сфер S^2k+1 × S^2k+1, k = 0, 1, 3, с выкинутой открытой клеткой, а все другие многообразия Кервера не гомеоморфны произведениям сфер с выкинутой клеткой.

В топологии многообразий часто используются PL-многообразия M̂^4k и K̂^4k, полученные добавлением конуса над краем, соответственно, многообразий Милнора M^4k и многообразий Кервера K^4k+2, а также два 4-мерных гладких многообразия - одно из них W⁴(T) (Т не обязательно дерево) является параллелизуемым односвязным многообразием, край к-рого диффеоморфен 3-сфере, а сигнатура равна 16. Такое многообразие Р⁴ = W⁴(Т) наз. многообразием (или плюмбингом) Рохлина. В известных примерах многообразий Рохлина минимальное значение двумерного числа Бетти равно 22. Другое многообразие есть W⁴(Г), где Г - граф, указанный выше, в качестве блока берется трубчатая окрестность диагонали в произведении S² × S². Край получающегося многообразия Q⁴ = W⁴(Г) есть неодносвязное додекаэдра пространство.

Трехмерные Д. м. M³ = ∂W⁴(T) принадлежат к так называемым многообразиям Зейферта. Не всякое 3-мерное многообразие является Д. м., и для Д. м. справедлива гипотеза Пуанкаре. В частности, 3-мерные линзовые пространства получаются от склейки только двух блоков.

Лит.: [i] Кеrvairе М., «Comment. math. helv.», 1960, v. 34, p. 257-70; [2] Кervaire M., Milnor J., «Ann. Math.», 1963, v. 77, № 3, p. 504-37; [3] Mилнор Дж., «Успехи матем. наук», 1965, т. 20, в. 6, с. 41-54; [4] Нirzebruch F., Neumann W. D., Кoh S. S., Differentieble manifolds and quadratic forms, N. Y., 1971; [5] Вrоwder W., Surgery on simply-conuected manifolds, В., 1972.

M. А. Штанько.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.