ДОМИНИРОВАНИЕ

ДОМИНИРОВАНИЕ - 1) Какое-либо из возможных соотношений порядка для дифференциальных операторов, формулируемое в терминах характеристического многочлена Р(ξ). Напр., если

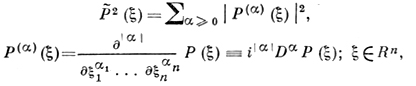
то P(D) сильнее Q(D), когда для любого ξ ∈ Rⁿ

Q̃(ξ)/P̃(ξ) < const.

Существуют и другие определения Д. (см. [1], с. 99, 103).

Лит.: [1] Хёрмандер Л., Линейные дифференциальные операторы с частными производными, пер. с англ., М., 1965.

А. А. Дезик.

2) Д. в теории игр - отношение, выражающее превосходство одного объекта (стратегии, дележа) над другим. Д. стратегий: стратегия s игрока i доминирует (строго доминирует) его стратегию t, если его выигрыш в каждой ситуации, содержащей s, не меньше (соответственно больше), чем его выигрыш в ситуации, состоящей из тех же стратегий остальных игроков и стратегии t. Д. дележей (в кооперативных играх): дележ х доминирует дележ у (обозначение х ≻ у), если существует такая непустая коалиция P ⊂ N, что

∑_i∈P x_i ≤ v(P)

и x_i > y_i для i ∈ P (v - характеристическая функция игры).

И. Н. Врублевская.

3) Д. в теории потенциала - отношение порядка v₁ ≥ v₂ между функциями, в частности потенциалами определенных классов, т. е. выполнение неравенства v₁(x) ≥ v₂(x) для всех х в общей области определения v₁ и v₂. В различных принципах доминирования отношение v₁ ≥ v₂ устанавливается как следствие выполнения неравенства v₁(х) ≥ v₂(x) на нек-рых собственных подмножествах области определения. Простейший принцип доминирования Картана: пусть v = v(x) - неотрицательная супергармоническая функция (см. Субгармоническая функция) на евклидовом пространстве ℝⁿ n #&8805; 3, и U_μ = U_μ(х) - ньютонов потенциал меры μ ≥ 0 конечной энергии (см. Энергия мер). Тогда, если v(x) ≥ U_μ(x) на нек-ром множестве A ⊂ ℝⁿ таком, что μ(CA) = 0, то имеет место Д. v ≥ U_μ. См. также Потенциала теория абстрактная.

Лит.: [1] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964; [2] его же, О топологиях и границах в теории потенциала, пер. с англ., М., 1974.

Е. Д. Соломенцев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.