ДОВЕРИТЕЛЬНОЕ ОЦЕНИВАНИЕ

ДОВЕРИТЕЛЬНОЕ ОЦЕНИВАНИЕ - метод математич. статистики, предназначенный для построения множества приближенных значений неизвестных параметров вероятностных распределений. Пусть X - случайный вектор, принимающий значения на множестве X в евклидовом пространстве, причем распределение вероятностей этого вектора принадлежит параметрич. семейству распределений, заданному плотностями p(x|θ), x ∈ X, θ ∈ Θ, относительно нек-рой меры μ(x). Предполагается, что истинное значение параметрич. точки θ, соответствующей результату наблюдений X, неизвестно. Суть Д. о. заключается в построении такого множества С(Х), зависящего от X, к-рое содержит значение заданной функции u(θ), соответствующее неизвестному истинному значению параметрич. точки θ. Пусть U - множество значений функции u(θ), θ ∈ Θ, и пусть С(х), x ∈ X, - какая-либо совокупность множеств, принадлежащих U при всех х из X, причем предполагается, что для произвольного элемента u ∈ U и любого значения θ ∈ Θ в определена вероятность события {с(Х) ∋ u}. Эта вероятность выражается интегралом

P_C(u, θ) = ∫_C(x)∋u p(x|θ) dμ(x), u ∈ U, θ ∈ Θ

и наз. вероятностью накрытия множеством C(X) значения и при заданном значении 0.

Если истинное значение θ неизвестно, то множество C(X) (из совокупности множеств С(х), х ∈ X), соответствующее результату наблюдений X, наз. доверительным множеством, или интервальной оценкой, для неизвестного истинного значения функции u(θ). В качестве вероятностной характеристики интервальной оценки C(X), построенной по указанному правилу, используется доверительная вероятность Р_C(θ), выражающаяся в терминах вероятности накрытия равенством

Р_C(θ) = Р_C[u(θ), θ], θ ∈ Θ.

Иными словами, Р_C(θ) - вероятность накрытия множеством С(X) значения заданной функции u(θ), соответствующего неизвестной истинной параметрич. точке θ.

В тех случаях, когда доверительная вероятность Р_C(θ) от θ не зависит, интервальную оценку C(X) наз. подобной пространству выборок. Это название обусловлено аналогией формул

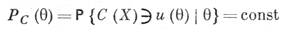
и

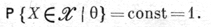
В более общей ситуации P_C(θ) зависит от неизвестного θ, и поэтому в практич. работе принято характеризовать качество интервальной оценки коэффициентом доверия

P_C = inf Р_C(θ),

где нижняя грань вычисляется на множестве в (иногда коэффициент доверия наз. доверительным уровнем).

Оптимизация Д. о. определяется теми требованиями, к-рые предъявляются к интервальным оценкам. Напр., если цель заключается в построении доверительных множеств, подобных пространству выборок и имеющих заданный коэффициент доверия ω (0,5 ≤ ω < 1), то первое требование выражается тождеством

P_C[u(θ), θ] = ω, θ ∈ Θ.

При этом естественно искать такие интервальные оценки, к-рые накрывают истинное значение u(θ) с вероятностью, не меньшей вероятности накрытия любого произвольного значения u ∈ U. Иными словами, второе требование, называемое требованием несмещенности, выражается неравенством

Р_C(u, θ) ≤ ω, u ∈ U, θ ∈ Θ.

В этих условиях «наилучшей» разумно считать ту интервальную оценку С, к-рая с меньшей вероятностью накрывает любое значение u, отличное от истинного u(θ). Отсюда возникает третье требование «наибольшей селективности»: для всякого другого доверительного множества С', отличного от С и удовлетворяющего условию

Р_C'[u(θ), θ] ≥ ω, θ ∈ Θ,

должно выполняться неравенство

Р_C(u, θ) ≤ P_C'(u, θ), u ∈ U, θ ∈ Θ.

Задача отыскания интервальных оценок С, удовлетворяющих указанным трем требованиям, эквивалентна задаче построения несмещенных, наиболее мощных статистич. критериев, подобных пространству выборок и имеющих уровень значимости 1 - ω. Вопросы существования решения такой задачи и его конструктивного описания составляют основу общей теории статистич. проверки гипотез.

Наиболее часто применяется Д. о. в ситуации, когда u(θ) - скалярная функция. Пусть X₁, ..., Х_n, n ≥ 2, - независимые случайные величины, подчиняющиеся одному и тому же нормальному распределению с неизвестными параметрами ∃ Х_i = θ₁ и ⅮX_i = θ₂, причем требуется построить интервальную оценку для u(θ) = θ₁. Пусть

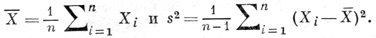
Поскольку случайная величина Т = √n(X̅ - θ₁)/s подчиняется Стьюдента распределению с n - 1 степенями свободы и это распределение не зависит от неизвестных параметров θ₁ и θ₂(|θ₁| < ∞, θ₂ > 0), то при любом положительном t вероятность события

{Х̅ - ts/√n < θ₁ < X̅ + ts/√n }

зависит лишь от t. Если указанный интервал принять за интервальную оценку С для θ₁, то ему будет соответствовать доверительная вероятность

P_C(θ₁, θ₂) = P{|T| < t},

не зависящая от θ = (θ₁, θ₂). Такую интервальную оценку наз. доверительным интервалом, а ее концевые точки - доверительными границами, или доверительными пределами, причем в данном случае доверительный интервал представляет собой интервальную оценку, подобную пространству выборок. В приведенном примере интервальная оценка является несмещенной и наиболее селективной.

Лит.: [1] Уилкс С., Математическая статистика, пер. с англ., М., 1967; [2] Шметтерер Л., Введение в математическую статистику, пер. с нем., М., 1976; [3] Леман Э., Проверка статистических гипотез, пер. с англ., М., 1964; [4] Большев Л. Н., «Теория вероят. и ее примен.», 1965, т. 10, в. 1, с. 187-92.

Ю. В. Линник, Н. М. Халфина.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.