ДЛИНА

ДЛИНА - числовая характеристика протяженности линий в метрич. пространстве. Д. отрезка прямой - расстояние между его концами, измеренное каким-либо отрезком, принятым за единицу Д. Длина ломаной - сумма Д. ее звеньев. Д. простой дуги - точная верхняя грань длин ломаных, вписанных в эту дугу. Всякая непрерывная кривая имеет Д. - конечную или бесконечную. Если ее Д. конечна, то кривая наз. спрямляемой. Д. плоской кривой, заданной в прямоугольных координатах уравнением y = f(x), a ≤ x ≤ b (f(x) имеет непрерывную производную f'(x)), выражается интегралом

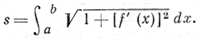
Если кривая задана в параметрич. форме

x = x(t), y = y(t), t₁ ≤ t ≤ t₂,

то Д. кривой равна

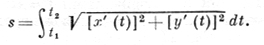
Д. спрямляемой кривой не зависит от параметризации. Д. пространственной кривой, заданной в параметрич. форме x = x(t), y = y(t), z = z(t), t₁ ≤ t ≤ t₂, выражается формулой

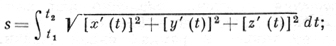
в случае n-мерного пространства

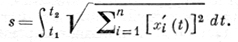
Пусть γ - непрерывно дифференцируемая кривая, заданная функциями u = u(t), v = v(t), на непрерывно дифференцируемой поверхности r = r(u, v). Тогда длина дуги кривой от точки, соответствующей значению параметра t = t₀, равна

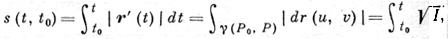
где I - первая квадратичная форма поверхности. Д. непрерывно дифференцируемой кривой, заданной функциями xⁱ = xⁱ(t), t₁ ≤ t ≤ t₂, в римановом пространстве с метрич. тензором g_ik, равна

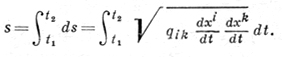
А. Б. Иванов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.