ДИФФУЗИОННЫЙ ПРОЦЕСС

ДИФФУЗИОННЫЙ ПРОЦЕСС - непрерывный

.марковский процесс X = X(t) с переходной плотностью p(s, х, t, у), удовлетворяющей следующим условиям: существуют функции a(t, х) и σ²(t, х), называемые соответственно коэффициентами сноса и диффузии, такие, что для любого ε > 0

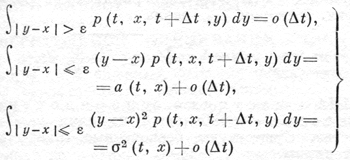
(1)

(причем обычно предполагается, что эти предельные соотношения выполняются равномерно по t в каждом конечном интервале t₀ ≤ t ≤ t₁ и по х, - ∞ < x < ∞). Важнейшим представителем этого класса процессов является процесс броуновского движения, впервые рассмотренный как математич. модель процессов диффузии (отсюда и название «Д. п.»). Если переходная плотность р(s, х, t, y) непрерывна

по s и х вместе со своими производными ∂/∂x р(s, х, t, у)

и ∂²/∂x² р(s, х, t, у), то она является фундаментальным решением дифференциального уравнения

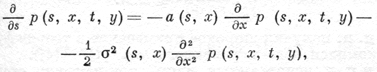
(2)

к-рое наз. обратным уравнением Колмогорова.

В однородном случае, когда коэффициенты сноса a(t, х) = а(х) и диффузии σ²(t, х) = σ²(х) не зависят от времени t, обратное уравнение Колмогорова для соответствующей переходной плотности р(s, х, t, у) = p(t - s, х, у) имеет вид:

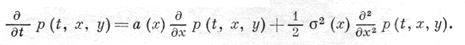
Если переходная плотность р(s, х, t, у) имеет непрерывную по t н у производную ∂/∂t р(s, х, t, у) такую, что

функции ∂/∂y [а(t, y) p(s, х, t, у)] и ∂²/∂y² [σ²(t, y) p(s, х, t, y)]

непрерывны по у, то она является фундаментальным решением дифференциального уравнения

∂/∂t р(s, х, t, у) = -∂/∂y [a(t, у) р(s, х, t, у)] + 1/2 ∂²/∂y² [σ²(t, y) p(s, x, t, y)], (3)

к-рое наз. уравнением Фоккера-Планка, или прямым уравнением Колмогорова. Дифференциальные уравнения (2) и (3) для плотности вероятности являются основой аналитич. методов изучения Д. п. Существует и другой, чисто «вероятностный», подход к Д. п., основанный на представлении процесса X(t) как решения стохастического дифференциального уравнения Ито

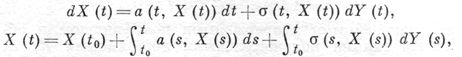
где Y(t) - стандартный процесс броуновского движения. Грубо говоря, при таком подходе считают X(t) связанным с нек-рым процессом броуновского движения Y(t) таким образом, что при условии X(t) = x за последующее время At приращение ΔX(t) = = X(t + Δt) - X(t) есть

ΔХ(t) ~ а(t, х)Δt + σ(t, х) ΔY(t).

Если понимать это асимптотич. соотношение в том смысле, что

∃ {ΔХ(t) - (a(t, х)Δt - σ(t, х) ΔY(t)) | X(t) = x} = o(Δt),

∃ {ΔХ(t) - (a(t, х)Δt + σ(t, х) ΔY(t))² | X(t) = x} = -o(Δt),

где o(Δt) - величины того же типа, что и в равенствах (1), то рассматриваемый процесс X(t) будет диффузионным и в смысле этого определения.

Многомерным Д. п. обычно наз. непрерывный марковский процесс X(t) = {X₁(t), ..., X_n(t)} в n-мерном векторном пространстве Еⁿ, переходная плотность р(s, х, t, у) к-рого удовлетворяет следующим условиям: для любого ε > 0

∫_|y-x|>ε p(t, x, t + Δt, y) dy = o(Δt),

∫_|y-x|≤ε (y_k - x_k) p(t, x, t + Δt, y) dy = a_k(t, x) Δt + o(Δt),

∫_|y-x|≤ε (y_k - x_k)(y_j - x_j) p(t, x, t + Δt, y)dy = 2b_kj(t, x)Δt + o(Δt),

k, j = 1, ..., n, x = (x₁, ..., x_n), y = (y₁, ..., y_n).

Вектор a = {a₁(t, x), ..., a_n(t, x)} характеризует локальный снос процесса ξ(t), матрица σ² = ||2b_kj(t, х)||, k, j = 1, ..., n, характеризует среднеквадратичное отклонение случайного процесса ξ(t) от исходного положения х за малый промежуток времени от t до t + Δt.

При нек-рых дополнительных ограничениях переходная плотность р(s, х, t, у) многомерного Д. п. удовлетворяет обратному и прямому дифференциальным уравнениям Колмогорова:

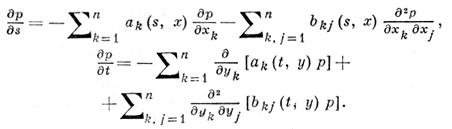
Многомерный Д. п. А (г) может быть описан также при помощи стохастических дифференциальных уравнений Ито:

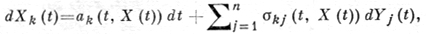
где Y₁(t), ..., Y_n(t) - взаимно независимые процессы броуновского движения, а

σ_j = {σ_1j(t, x), ..., σ_nj(t, x)}, j = 1, ..., n,

суть собственные векторы матрицы σ² = ||2b_kj(t, х)||.

Лит.: [1] Гихман И. И., Скороход А. В., Введение в теорию случайных процессов, М., 1965; [2] их же, Стохастические дифференциальные уравнения, К., 1968.

Ю. А. Розанов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.