ДИФФЕРЕНЦИРУЕМОЕ МНОГООБРАЗИЕ

ДИФФЕРЕНЦИРУЕМОЕ МНОГООБРАЗИЕ - локально евклидово пространство, наделенное дифференциальной структурой.

Пусть X - хаусдорфово топологич. пространство. Если для каждой точки х ∈ X найдется ее окрестность U, гомеоморфная открытому множеству пространства ℝⁿ, то X наз. локально евклидовым пространством, или топологическим многообразием размерности п. Пара (U, φ), где φ -указанный гомеоморфизм, называется локальной картой X в точке х. Таким образом, каждой точке соответствует набор n действительных чисел (х₁, ..., х_n), называемых координатами x в карте (U, φ).

Семейство карт {(U_α, φ_α)}, α ∈ A, наз. n-мерным С^k-атласом (0 ≤ k ≤ ∞, а) многообразия X, если: а) совокупность всех U_α покрывает X, Х= (∪_α∈A U_α; б) для любых α, β ∈ A таких, что U_α ∩ U_β ≠ ∅, отображение

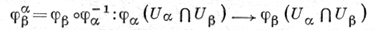
принадлежит дифференцируемости классу C^k; φ^α_β является дифференцируемым отображением с отличным от нуля якобианом и наз. преобразованием координат точки х из карты (U_α, φ_α) в карту (U_β, φ_β).

Два С^k-атласа наз. эквивалентными, если их объединение снова является С^k-атласом. Совокупность С^k-атласов разбивается на классы эквивалентности, к-рые наз. C^k-структурами, при 1 ≤ k ≤ ∞ - дифференциальными (или гладкими) структурами, при k = а -аналитическими структурами. Топологич. многообразие X, наделенное С^k-структурой, называется С^k-многообразием, или дифференцируемым многообразием класса C^k.

Понятие дифференциальной структуры можно ввести для произвольного множества X, заменив гомеоморфизмы φ_α биективными отображениями на открытые множества ℝⁿ; при этом топология С^k-многообразия описывается как топология объединения, построенная по любому атласу соответствующей структуры. В этом случае n-мерные многообразия обладают очевидной n-мерной С⁰-структурой.

Задачи аналитич. и алгебраич. геометрии приводят к необходимости рассматривать в определении дифференциальной структуры вместо пространства ℝⁿ более общие пространства ℂⁿ или даже Кⁿ, где К -полное недискретное нормированное поле. Так, в случае K = ℂ соответствующая С^k-структура, k ≥ 1, непременно оказывается С^a-структурой, она наз. комплексно аналитической, или просто комплексной, а соответствующее Д. м.- комплексным многообразием. При этом на любом таком многообразии есть и естественная действительная С^a-структура.

На любом С^a-многообразии есть согласованная с ней С^∞-структура, и на С^k-многообразии, 0 ≤ k ≤ ∞, -С^r-структура, если 0 ≤ r ≤ k. Обратно, любое паракомпактное С^r-многообразие, r ≥ 1, можно наделить С^a-структурой, совместимой с заданной, причем эта структура (с точностью до изоморфизма, см. ниже) единственна. Может, однако, случиться, что С⁰-многообразие нельзя снабдить C¹-структурой (т. е. существуют несглаживаемые многообразия), а если это удается, то такая структура неединственна. Например, число θ(n) C¹-неизоморфных С^∞-структур на n-мерной сфере таково:

n 1 2 3 4 5 6 7 8 9 10 11 12

θ(n) 1 1 1 ? 1 1 28 2 8 6 992 1

Пусть f: X → Y - непрерывное отображение C^r-многообразий X, Y; оно наз. C^k- морфизмом (или C^k-отображением, k ≤ r, или отображением класса C^k) Д. м., если для любой пары карт (U_α, φ_α) на Х и (V_β, ψ_β) на Y такой, что f(U_α) ⊂ V_β, отображение

ψ_α ○ f ○ φ^-1_β : φ_α(U_α) → ψ_β(V_β) принадлежит классу C^k. Биективное отображение f такое, что оно и f^-1 суть Сⁿ-отображения, наз. Сⁿ - изоморфизмом (или диффеоморфизмом) класса Сⁿ. В этом случае X и Y и определяющие их С^r-структуры наз. Сⁿ-изоморфными.

Подпространство Y n-мерного С^k-многообразия X наз. С^k-подмногообразием размерности m в X, если для всякой точки y ∈ Y существуют ее окрестность V ⊂ Y и карта (U, φ) С^k-структуры X такие, что V ⊂ U и φ индуцирует гомеоморфизм V на пересечение φ(U ∪ Y) с (замкнутым) подпространством ℝ^m ⊂ ℝⁿ; другими словами, существует карта с координатами х¹, ..., хⁿ такая, что U ∪ Y определяется соотношениями х^m+1 = ... = хⁿ = 0.

Отображение f : X → Y наз. C^k - вложением, если f(Х) есть С^k-подмногообразие в Y, а X → f(X) - С^k-диффеоморфизм. Всякое n-мерное C^k-многообразие допускает вложение в ℝ²ⁿ⁺¹ и даже в ℝ²ⁿ. Более того, множество таких вложений является всюду плотным в пространстве отображений С^k(Х, ℝ²ⁿ⁺¹) относительно компактно-открытой топологии. Тем самым, рассмотрение Д. м. как подмногообразий евклидова пространства дает один из способов изложения их теории, на этом пути устанавливаются, напр., указанные выше теоремы о С^a-струк-турах.

В топологии Д. м., иначе наз. дифференциальной топологией, - две основные проблемы. Первая - задача классификации Д. м. Существуют три основных класса Д. м.- замкнутые, компактные многообразия с краем и открытые. Важными инвариантами, различающими Д. м., являются гомотопический тип и касательное расслоение, в частности характеристические классы. С их помощью проведена классификация гладких структур для односвязных многообразий данного гомотопич. типа. С помощью другого инварианта - класса бордизма Д. м.- решена обобщенная Пуанкаре гипотеза, изучены неподвижные точки при действии группы на многообразии и т. д. При этом потребовалось введение дифференциальных структур на многообразиях с краем и аппарата сглаживания. Наконец, полезными здесь оказываются методы алгебраич. топологии, поскольку, напр., установлена триангулируемость произвольного С'-многообразия.

Вторая - задача классификации отображений Д. м. Прежде всего здесь выделяются классы иммерсий, или погружений, обобщающих вложения; их классификация сведена к гомотопич. задаче в отличие от вложений, полная классификация к-рых не получена (1978) (см. Топология вложений), и субмерсий, или расслоений, одного Д. м. в (на) другое. Важную роль, в частности, в вопросах устойчивости (стабильности) и в исследовании типичных особенностей отображений играет понятие трансверсальности отображения вдоль подмногообразия. Существование трансверсальных отображений обеспечивается теоремами типа Сарда теоремы. Все это, а также задачи дифференциальной динамики, изучающей строение различных групп диффеоморфизмов, в частности интегральных траекторий и особых точек векторных полей на д. м. (динамических систем), и различные отношения эквивалентности: изотопия, топологическая и С^k-сопряженность и т. п.. - диктует необходимость рассмотрения, наряду с конечномерными пространствами ℝⁿ, произвольных банаховых (или гильбертовых) пространств и определения соответствующих дифференциальных структур. При этом требуется выполнение разумных в отношении приложений дополнительных условий, напр. Д. м. отделимо тогда и только тогда, когда преобразования координат имеют замкнутый график. Получающиеся наделением такой структурой, вообще говоря, бесконечномерные многообразия, соответственно именуемые банаховыми (или гильбертовыми) многообразиями, типичным примером к-рых служат многообразия отображений конечномерных Д. м., оказываются полезным средством исследования и геометрич. интерпретацией задач аппроксимации отображений (как в указанной выше теореме вложения), анализа петель пространства - надлежащей области для построения теории Морса и т. д.

Д. м. являются естественной базой для построения дифференциальной геометрии. Там на Д. м. вводятся дополнительные инфинитезимальные структуры - ориентации, метрика, связность и т. д., и изучаются те свойства, связанные с этими объектами, к-рые инвариантны относительно группы диффеоморфизмов, сохраняющих дополнительную структуру. С другой стороны, использование той или иной структуры позволяет исследовать строение самого Д. м. Простейший пример - выражение характеристич. классов через кривизну Д. м., наделенного линейной связностью.

Лит.: [1] Понтрягин Л. С., Гладкие многообразия и их применения в теории гомотопий, 2 изд., М., 1976; [2] Бурбаки Н., Дифференцируемые и аналитические многообразия. Сводка результатов, пер. с франц., М., 1975; [3] де Рам Ж., Дифференцируемые многообразия, пер. с франц., М., 1956; [4] Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., Ы., 1967; [5] Рохлин В. А., Фукс Д. Б., Начальный курс топологии. Геометрические главы, М., 1977; [6] Уитни X., Геометрическая теория интегрирования, пер. с англ., М., 1960; [7] Постников М. М., Введение в теорию Морса, М., 1971; [8] Нарасимхан Р., Анализ на действительных и комплексных многообразиях, пер. с англ., М., 1971; [9] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976; [10] Голубицкий М., Гийемин В., Устойчивые отображения и их особенности, пер. с англ., М., 1977; [11] Брекер Т., Ландер Л., Дифференцируемые ростки и катастрофы, пер. с англ., М., 1977; [12] Нитецки З., Введение в дифференциальную динамику, пер. с англ., М., 1975; [13] Стернберг С., Лекции по дифференциальной геометрии, пер. с англ., М., 1970; [14] Годбийон К., Дифференциальная геометрия и аналитическая механика, пер. с франц., М., 1973; [15] Зуланке Р., Винтген П., Дифференциальная геометрия и расслоения, пер. с нем., М., 1975.

См. также лит. при статье Дифференциальная топология.

М. И. Войцеховский.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.