ДИФФЕРЕНЦИРОВАНИЕ ЧИСЛЕННОЕ

ДИФФЕРЕНЦИРОВАНИЕ ЧИСЛЕННОЕ - нахождение производной функции численными методами. Д. ч. используется в случаях, когда методы дифференциального исчисления неприменимы (функция задана таблично), или их применение вызывает значительные трудности (функция имеет сложное аналитическое выражение).

Пусть на отрезке [а, b] определена функция u = u(х) и заданы узловые точки х_i, а = х₁ < х₂ < ... < х_n = b. Совокупность точек (x_i, u_i = u(x_i)), i = 1, ..., n, наз. таблицей. Результатом Д. ч. таблицы является функция u^k_n(х), в каком-либо смысле приближающая k-ю производную d^ku(x)/dx^k функции па нек-ром множестве Х^k_n точек х. Применение Д. ч. целесообразно, когда получение функции u^k_n(x) для каждого х ∈ Х^k_n требует незначительной затраты вычислительных средств. Обычно используются линейные методы Д. ч., где результат Д. ч. записывается в виде

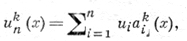
а^k_i(х) - функции, определенные на Х^k_n. Наиболее распространенный метод получения формул (1) состоит в следующем: строят функцию

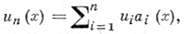
интерполирующую u(х), и полагают

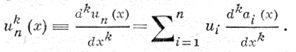
Точность алгоритмов, основанных на интерполяционных формулах Лагранжа, Ньютона и др., существенным образом определяется выбором способа интерполяции и может быть иногда весьма низкой даже для достаточно гладких функций u = u(х) и при большом числе узловых точек (см. [1]). От этого недостатка часто свободны алгоритмы Д. ч., использующие сплайн-интерполяцию (см. [2]). Если требуется вычисление приближенных значений производной только в узловых точках х_i, то формула (1) принимает вид

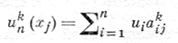
(2)

и u^k_n(x_j) полностью определяется заданием для данного к матрицы коэффициентов а^k_ij. Формулы типа (2) наз. разностными формулами Д. я. Коэффициенты a^k_ij этих формул определяют из условия наивысшего порядка малости по h_n = mах_ij |х_i+1 + x_i| разности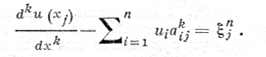

Формулы (2), как правило, весьма просты и удобны на практике. Напр., при h = h_n = (x₂ - х₁) = (х₃ - х₂) = ... = (х_n - x_n-1) они имеют вид:

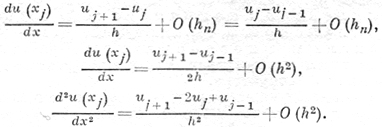
Алгоритмы Д. ч. часто применяются к таким таблицам, в к-рых значения u(x_i) заданы (или получены) неточно. В этом случае требуется их предварительное сглаживание, так как непосредственное применение Д. ч. может привести к большим погрешностям в результатах (см. [3]).

Лит.: [1] Березин И. С., Жидков Н. П., Методы вычислений, 3 изд., т. 1, М., 1966; [2] Альберг Дж., Нильсон Э., Уолш Дж., Теория сплайнов и ее приложения, пер. с англ., М., 1972; [3] Морозов В. А., в кн.: Вычислительные методы и программирование, в. 14, М., 1970, с. 46-62.

В. А. Морозов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.