ДИФФЕРЕНЦИРОВАНИЕ ПО СЕТИ

ДИФФЕРЕНЦИРОВАНИЕ ПО СЕТИ - специальное понятие дифференцирования функций множеств ψ(E). Сеть N - совокупность разбиений {Аⁱ_j} основного пространства X с мерой μ, при этом

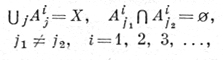
и для каждого Аⁱ⁺¹_j1 найдется содержащее его множество Аⁱ_j2. Все Аⁱ_j измеримы и их совокупность в определенном смысле (см. [1]) аппроксимирует все измеримые множества. Множества Аⁱ_j при фиксированном i наз. множествами i-гo ранга. Для каждой точки х₀ и любого n имеется одно и только одно множество А_n(х₀) n-го ранга, содержащее точку х₀.

Производной функции ψ(Е) по данной сети N в точке x₀ наз. выражение

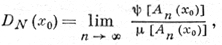
если этот предел существует. Можно также определить понятие производных чисел по сети N.

Простейшим примером Д. по с. служит дифференцирование приращения функции одного действительного переменного по двоично-рациональным интервалам вида (j/2ⁱ, (j + 1)/2ⁱ].

Производная по сети для каждой счетно аддитивной функции ψ(E) существует почти всюду и совпадает с плотностью абсолютно непрерывной составляющей функции ψ(E). В n-мерном пространстве обычно рассматривается Д. по с. полуоткрытых сегментов, диаметр к-рых стремится к нулю с ростом ранга (см. [2]).

Понятие сети и дифференцирования по ней может быть обобщено на случай абстрактных пространств без меры (см. [3]).

Лит.: [1] Шилов Г. Е., Гуревич Б. Л., Интеграл, мера и производная, 2 изд., М., 1967; [2] Сакс С., Теория интеграла, пер. с англ., М., 1949; [3] Кenyon Н., Morse А. P., Web derivatives, N. Y., 1973 («Меm. Аmеr. Math. Soc.», № 132).

В. А. Скворцов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.