ДИФФЕРЕНЦИРОВАНИЕ

ДИФФЕРЕНЦИРОВАНИЕ кольца - отображение ∂ кольца R в себя, являющееся эндоморфизмом аддитивной группы кольца R и удовлетворяющее соотношению

∂(х⋅у) = х∂(у) + ∂(х)у.

Пусть М - левый R-модуль. Дифференцированием кольца R со значениями в М наз. гомоморфизм соответствующих аддитивных групп, удовлетворяющий условию

∂(х⋅у) = х∂(у) + y∂(х)

для всех х, у из R. Для любого элемента с из центра С кольца R отображение х → с∂(х), где ∂ - дифференцирование, является Д. Сумма двух дифференцирований также является Д. Это определяет на множестве всех Д. кольца R со значениями в М структуру С-модуля, обозначаемого Der(R, М). Если S подкольцо в R, то Д. ∂ такое, что ∂(s) = 0 для всех s ∈ S наз. S-дифференцированием. Множество всех S-дифференцирований образует подмодуль в Der(R, М), обозначаемый Der_S(R, М). Операция

[∂, ∂'] = ∂ ○ ∂' - ∂' ○ ∂

определяет в S-модуле Der_S(R, М) структуру ,S-алгебры Ли. Если φ: R → M - гомоморфизм R-модулей, то для любого ∂ ∈ Der(R, R) композиция φ ○ ∂ ∈ Der(R, М).

Пусть R - кольцо полиномов А[Т₁, ..., Т_n] с коэффициентами в коммутативном кольце А. Отображение

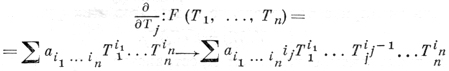
является A-дифференцированием кольца R, a R-модуль Der_A(R, R) - свободным модулем с базисом ∂/∂Т₁, ..., ∂/∂Т_n.

Для любого элемента a ассоциативного (соответственно лиева) кольца R отображение х → ах - ха (соответственно х → ах) будет Д. кольца R, наз. внутренним дифференцированием. Д., не являющееся внутренним, наз. внешним.

Если R - подкольцо кольца R' и ∂ ∈ Der(R, R), то говорят, что ∂̅ ∈ Der(R', R') продолжает ∂, когда ограничение ∂̅ на R совпадает с д. В случае, когда R - коммутативное целостное кольцо, а R'- его поле частных, а также в случаях, когда R'- сепарабельное алгебраич. расширение поля R или R - алгебра Ли над полем k, a R'- ее обертывающая алгебра, существует единственное продолжение любого Д. ∂: R → R на R'.

Имеется тесная связь между Д. и изоморфизмами колец. Напр., если ∂ - нильпотентное Д., т. е. ∂ⁿ = 0, и R - алгебра над полем характеристики нуль, то отображение

exp(∂) = 1 + ∂ + ∂²/2! + ... + ∂^n-1/(n-1)!

является автоморфизмом k-алгебры R. Если R - локальное коммутативное кольцо с максимальным идеалом 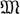, то имеет место биекция между множеством Д. Der(R, R/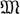) и множеством автоморфизмов кольца R/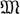², индуцирующих тождественный автоморфизм поля вычетов R/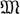. Д. несепарабельных расширений полей играют роль элементов группы Галуа сепарабельных расширений в теории Галуа таких расширений [4].

Лит.: [1] Бурбаки Н., Алгебра. Многочлены и поля. Упорядоченные группы, пер. с франц., М., 1965; [2] Джекобсон Н., Теория колец, пер. с англ., М., 1947; [3] Ленг С., Алгебра, пер. с англ., М., 1968; [4] Моrdеsоn J., Vinograde В., Structure of arbitrary purely inseparable extension fields, В., 1970.

И. В. Долгачев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.