ДИФФЕРЕНЦИАЛЬНЫЙ ПАРАМЕТР

ДИФФЕРЕНЦИАЛЬНЫЙ ПАРАМЕТР, диффeренциатор, - совместный дифференциальный инвариант одной или нескольких функций и метрич. тензора g_ij римановой геометрии. Д. п. 1-го порядка (первый Д. п.) функции V есть квадрат ее градиента:

Δ₁V = g^ijV_iV_j.

Смешанный Д. п. 1-го порядка функций V и W есть скалярное произведение градиентов этих функций

Δ₁(V, W) = g^ijV_iW_j.

В трехмерном евклидовом пространстве в декартовой прямоугольной системе координат эти Д. п. выражаются формулами:

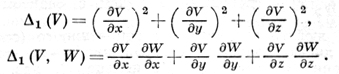
Д. п. 2-го порядка (второй Д. п.) функции есть дивергенция ее градиента:

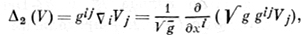
где g - определитель матрицы ||g_ij||. В трехмерном евклидовом пространстве в декартовой прямоугольной системе координат второй Д. п. выражается формулой

Δ₂(V) =∂²V/∂x² + ∂²V/∂y² + ∂²V/∂z².

Первоначально Д. п. были введены Г. Ламе [1] в евклидовой геометрии. Обобщение этого понятия для римановой геометрии принадлежит Э. Бельтрами [2]. Поэтому Д. п. иногда наз. дифференциальными параметрами Ламе, или дифференциальными параметрами Бельтрами.

Лит.: [1] Lame G., Lecons sur les coordonnées curvilignes et leurs diverses applications, P., 1859; [2] Beltrami E., Ricerche di analisi applicata alla geometria, «G. mat. Battaglini», 1864, v. 2, 1865, v. 3; [3] Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 1-2, М.- Л., 1947-48; [4] Шуликовский В. И., Классическая дифференциальная геометрия в тензорном изложении, М., 1963.

В. И. Шуликовский.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.