ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР

ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР модуля -отображение модулей над коммутативным кольцом, являющееся аналогом понятия дифференциального оператора. Пусть R - коммутативное кольцо, S -подкольцо кольца R, N и М - два R-модуля. Гомоморфизм S-модулей D: N → M наз. дифференциальным оператором порядка ≤ m (m - неотрицательное целое), если для любого x ∈ R отображение D_x: N → M, определяемое формулой

D_x(n) = D(xn) - xD(n),

является Д. о. порядка ≤ m - 1. При этом Д. о. порядка 0 наз. гомоморфизм R-модулей N → M. Множество всех таких Д. о. образует подмодуль Diff^m_S(N, М) R-модуля всех гомоморфизмов S-модулей Hom_S(N, М). В частности,

Diff⁰_S (N, М) ≃ Ноm_R(N, М),

а фактормодуль

Diff¹_S(N, M)/Diff⁰_S(N, M)

изоморфен модулю S-дифференцирований Der_S(R, М) кольца R со значениями в М. Объединение Diff_S(М) возрастающего семейства подмодулей

Diff⁰_S(M, М) ⊂ Diff¹_S(M, М) ⊂ ...

является фильтрованным ассоциативным кольцом относительно операции композиции отображений. Это кольцо наз. кольцом дифференциальных операторов R-модуля М над подкольцом S, а соответствующее градуированное кольцо

Symb_S(M) = ⊕_i≥0 Symbⁱ_S(М),

где

Symbⁱ_S(M) = Diffⁱ_S(M, М)/Diff^i-1_S(М, М),

наз. кольцом символов. Образ Д. о. D ∈ Diffⁱ_S(М, М) в кольце Symbⁱ_S(M) наз. символом Д. о.

Если R является алгеброй над полем рациональных чисел и модуль дифференциалов Ω¹_R/S проективен, то существует изоморфизм S-алгебры Diff_S(R) и обертывающей алгебры алгебры Ли S-дифференцирований Der_S(R, R). В этом случае кольцо Symb_S(R) изоморфно симметрич. алгебре R-модуля Der(R, R).

Напр., пусть R = k[T] - кольцо многочленов над полем k; отображения ∂/∂Тⁱ: R → R, определяемые формулой

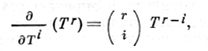
являются Д. о. кольца R над k порядка i. Кольцо Д. о. Diff_k(R) - свободный модуль над R с базой ∂/∂T⁰, ∂/∂T¹, ..., ∂/∂Tⁱ Умножение задается формулой

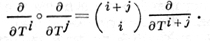
В частности,

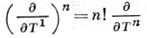
(формула Тейлора), что в случае, когда характеристика поля k равна 0, дает

Diff_k(R) ≅ R[∂/∂¹].

Если Spec(R) является аффинной групповой S-схемой, то можно рассматривать также инвариантные Д. о. кольца R (см. [2]).

Лит.: [1] Виноградов А. М., Красильщиков И. С., «Успехи матем. наук», 1975, т. 30, в. 1, с. 173-98; [2] Grothendieck A., Elements de géométrie algébrique, P., 1967, ch. 4; [3] Demazure M., Gabriel P., Groupes algébriques, t. 1, P.-Amst., 1970; [4] Björk J.-E. «Invent. Math.», 1972, v. 17, № 1, p. 67 - 78.

И. В. Долгачев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.