ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР

ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР - обобщение оператора дифференцирования. Д. о. (вообще говоря, не непрерывный, не ограниченный и не линейный) -оператор, определенный нек-рым дифференциальным выражением и действующий в пространствах (вообще говоря, векторнозначных) функций (или сечений дифференцируемых расслоений) на дифференцируемых многообразиях, или в пространствах, сопряженных к пространствам этого типа. Дифференциальное выражение - это такое отображение λ множества в пространстве сечений расслоения ξ с базой М в пространство сечений расслоения η с той же базой, что для любой точки р ∈ М и любых сечений f, g ∈ , из совпадений их k-струй в точке р следует совпадение λf и g в той же точке; наименьшее из чисел k, удовлетворяющих этому условию для всех р ∈ М, наз. порядком дифференциального выражения и порядком Д. о., определенного этим выражением.

На многообразии М без края Д. о. часто является расширением оператора, естественно определяемого фиксированным дифференциальным выражением на нек-ром (открытом в подходящей топологии) множестве бесконечно (или достаточно много раз) дифференцируемых сечений данного векторного расслоения ξ с базой М и, таким образом, допускает естественное обобщение на случай пучков ростков сечений дифференцируемых расслоений. На многообразии М с краем ∂М Д. о. L часто определяется как расширение аналогичного оператора, естественно определенного дифференциальным выражением на множестве тех дифференцируемых функций (или сечений расслоения), ограничения к-рых на ∂М лежат в ядре нек-рого Д. о. l на ∂М (или удовлетворяет каким-либо др. условиям, определяемым теми или иными требованиями к области значений оператора l на ограничениях функций из области определения оператора L, напр., неравенствами); Д. о. l наз. определяющим граничные условия для Д. о. L. Линейные Д. о. в пространствах, сопряженных к пространствам функций (или сечений), определяются как операторы, сопряженные к Д. о. указанного выше вида в этих пространствах.

Примеры. 1) Пусть F - действительная функция k + 2 переменных х, у₀, у₁, ..., у_k, определенная в нек-ром прямоугольнике Δ = I × J₀ × J₁ × ... × J_k; дифференциальное выражение

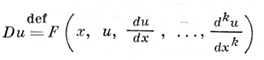
(где функция F обычно удовлетворяет нек-рым условиям регулярности - измеримости, непрерывности, дифференцируемости и т. п.) определяет Д. о. D на многообразии Д, область определения которого Ω состоит из всех функций u ∈ C^k(Δ), удовлетворяющих условию u⁽ⁱ⁾(x) ∈ J_i для i = 0, 1, ..., k; если F непрерывна, то D может рассматриваться как оператор в С(I) с областью определения Ω; Д. о. D наз. общим обыкновенным Д. о. Если F зависит от y_k, то порядок D равен k. Д. о. D наз. квазилинейным, если F линейно зависит от y_k; линейным, если F линейно зависит от у₀, y₁, ..., у_k; линейным с постоянными коэффициентами, если F не зависит от х и D является линейным Д. о. Остальные Д. о. наз. нелинейными. Квазилинейный Д. о. при нек-рых условиях регулярности

функции F может быть расширен до Д. о. из одного Соболева пространства в другое.

2) Пусть х = (х¹, ..., х^N) пробегает область 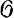в ℝ^N, F = F(x, u, D⁽ⁿ⁾(u)) - дифференциальное выражение, определяемое действительной функцией F на произведении области на нек-рый открытый прямоугольник со, здесь D⁽ⁿ⁾(u) - набор частных производных

вида D^αu = (∂^α₁+...+α_N)/((∂x¹)^α₁...(∂x^N)^α_N), где α₁ + ... + α_N ≤ n, а функция F (как и в 1) удовлетворяет нек-рым условиям регулярности. Определенный этим выражением Д. о. на пространстве достаточно дифференцируемых функций на × ω наз. общим Д. о. с частными производными. Аналогично 1) определяются нелинейные, квазилинейные и линейные Д. о. с частными производными и порядок Д. о.; Д. о. наз. эллиптическим, гиперболическим или параболическим, если он определяется дифференциальным выражением соответствующего типа. Иногда рассматриваются функции F, зависящие от производных всех порядков (напр., в виде формальной линейной комбинации их); таким дифференциальным выражениям, не определяющим Д. о. в обычном смысле, тем не менее могут быть сопоставлены нек-рые операторы (напр., в пространствах ростков аналитич. функций), наз. Д. о. бесконечного порядка.

3) Предыдущие примеры могут быть перенесены на случай комплексного поля, локально компактного вполне несвязного поля и (по крайней мере в случае линейных Д. о.) даже в более общую ситуацию, см. Дифференциальная алгебра.

4) Системы дифференциальных выражений определяют Д. о. в пространствах вектор-функций. Напр., Д. о. Коши-Римана, определенный дифференциальным выражением {∂u/∂x - ∂v/∂y, ∂u/∂y + ∂v/∂x}, преобразует пространство пар гармонических функций на плоскости в себя.

В определении Д. о. и его обобщений (кроме обычных производных) часто используются не только обобщенные производные (естественно возникающие при рассмотрении расширений Д. о., заданных на дифференцируемых функциях) и слабые производные (связанные с переходом к сопряженному оператору), но и производные дробного и отрицательного порядков. Более того, само дифференцирование заменяется преобразованием Фурье (или другим интегральным преобразованием), применяемым к области определения и значения такого обобщенного Д. о. (см. Псевдодифференциальный оператор) так, чтобы получить возможно более простое представление соответствующей Д. о. функции F и достичь разумной общности постановки задач и хороших свойств рассматриваемых объектов, а также построить функциональное или операционное исчисление (продолжающее соответствие между оператором дифференцирования и оператором умножения на независимую переменную, осуществляемое преобразованием Фурье).

Такие вопросы теории дифференциальных уравнений, как существование, единственность, регулярность, непрерывная зависимость решений от начальных данных или правой части, явный вид решения дифференциального уравнения, определенного данным дифференциальным выражением, естественно интерпретируются в терминах теории операторов как задачи Д. о., определенного данным дифференциальным выражением в подходящих функциональных пространствах, а именно - как задачи о ядре, образе, изучении структуры области определения данного Д. о. L или его расширения, непрерывности обратного оператора к данному Д. о. и явного построения этого обратного оператора. Вопросы аппроксимации решений и построения приближенных решений дифференциальных уравнений также находят естественное обобщение и усовершенствование в задачах о соответствующих Д. о., а именно - о подборе таких естественных топологий в области определения и области значений, чтобы оператор L (при условии единственности решений) осуществлял гомеоморфизм области определения и области значений в этих топологиях (эта теория связана с теорией интерполяции и шкал функциональных пространств, особенно в случаях линейных и квазилинейных Д. о.), или в подборе Д. о., близких к данному в том или ином смысле (что позволяет, используя различные топологии в множестве Д. о., обосновывать методы аппроксимации уравнений, в том числе метод регуляризации, метод штрафа и нек-рые итерационные методы регуляризации). Теория Д. о. позволяет применить классич. методы теории операторов, напр. теорию вполне непрерывных операторов, и метод сжатых отображений в различных теоремах существования и единственности решений дифференциальных уравнений, в теории бифуркации решений и в нелинейных задачах о собственных значениях. Часто оказывается возможным использовать наличие в функциональных пространствах, где определен Д. о., естественной структуры порядка (в частности, применить теорию монотонных операторов), использовать методы линейного анализа (теорию двойственности, теорию выпуклых множеств, теорию сопряженных операторов, теорию диссипативных операторов), вариационные методы и теорию экстремальных задач, а также наличие нек-рых дополнительных структур в области определения области значений (напр., комплексной, симплектической и т. д.) для выяснения структуры области значений и ядра Д. о., т. е. получения информации о классе решений соответствующих уравнений. Ряд задач, связанных с дифференциальными выражениями, приводит к необходимости изучения дифференциальных неравенств, естественно связанных с многозначными Д. о.

Таким образом, теория Д. о. позволяет разрешить ряд трудностей классич. теории дифференциальных уравнений. Использование различных расширений обычных Д. о. приводит к понятию обобщенного решения соответствующего дифференциального уравнения (к-рое в ряде случаев, связанных, напр., с эллиптич. задачами, оказывается необходимо классическим), а использование линейной структуры позволяет вводить понятие слабых решений дифференциальных уравнений. При выборе подходящего расширения Д. о., определенного дифференциальным выражением, важную роль играют связанные с конкретным видом последнего априорные оценки для решений, к-рые позволяют указать такие функциональные пространства, что в этих пространствах Д. о. непрерывен или ограничен.

Но теория Д. о. дает возможность поставить и решить и ряд принципиально новых задач по сравнению с классич. задачами теории дифференциальных уравнений. Так, для нелинейных операторов представляют интерес изучение структуры множества его неподвижных точек и действие оператора в их окрестности, а также классификация этих особых точек и вопрос об устойчивости типа особой точки при возмущении данного Д. о.; для линейных Д. о., кроме указанных выше задач, представляют интерес задачи об описании и изучении спектра Д. о., построения его резольвенты, вычислений индекса, описание структуры инвариантных подпространств данного Д. о., построение связанного с данным Д. о. гармонич. анализа (в частности, разложения по собственным функциям, что требует предварительного изучения вопросов полноты системы собственных и присоединенных функций), изучения линейных и нелинейных возмущений данного Д. о. Эти задачи представляют особый интерес для эллиптич. Д. о., порожденных симметричными дифференциальными выражениями, в связи с теорией самосопряженных операторов в гильбертовом пространстве (в частности, со спектральной теоремой для таких операторов и теорией расширений симметрия, операторов). Теория ряда задач гиперболических и параболических (не обязательно линейных) Д. о. связана с теорией групп и полугрупп преобразований локально выпуклых пространств.

Пожалуй, наиболее исследованный (помимо линейных) класс Д. о., к тому же имеющий широкое практич. применение, - Д. о., не изменяющиеся вообще или меняющиеся по вполне определенному закону при действии на область их определения и соответствующим образом на дифференциальное выражение нек-рых преобразований, составляющих группу G (или полугруппу). Таковы, напр., инвариантные дифференциальные операторы, тесно связанные с представлениями группы G; ковариантная производная или, более общо, пульверизация - Д. о. на пространствах дифференцируемых тензорных полей (здесь G группа всех дифферморфизмов), длинный ряд операторов теоретич. физики и т. п. Функционально-геометрич. методы полезны и при исследовании Д. о. с так наз. скрытой симметрией (см., напр., Кортевега-де-Фриза уравнение).

Теория Д. о., являющаяся составной частью общей теории операторов, играет в последнее время все более значительную роль не только в теории дифференциальных уравнений, но и вообще в современном анализе, причем не только как важный конкретный пример неограниченных операторов (это в особенности касается теории линейных Д. о.), но и как аппарат представления и средство изучения объектов различной природы: так, напр., любая обобщенная функция (и даже гиперфункция) получается действием нек-рого обобщенного Д. о. на непрерывную функцию. Наконец, непрерывно возрастает роль и влияние теории Д. о. в других разделах математики - напр., одно из решений так наз. проблемы индекса (см. Индекса формулы) связывает топологич. характеристики многообразия с наличием на нем определенного класса Д. о., что позволяет сделать заключение о свойствах эллиптич. комплексов на этом многообразии.

Лит.: [1] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [2] Наймарк М. А., Линейные дифференциальные операторы, 2 изд., М., 1969; [3] Xёрмандер Л., Линейные дифференциальные операторы с частными производными, пер. с англ., М., 1965; [4] Бурбаки Н., Дифференцируемые и аналитические многообразия. Сводка результатов, пер. сфранц., М., 1975; [5] Канторович Л. В., Акилов Г. П., Функциональный анализ, 2 изд., М., 1977; [6] Пале Р., Семинар по теореме Атьи-Зингера об индексе, пер. с англ., М., 1970; [7] Рейссиг Р., Сансоне Г., Конти Р., Качественная теория нелинейных дифференциальных уравнений, пер. с нем., М., 1974; [8] Фиников С. П., Метод внешних форм Картана в дифференциальной геометрии, М.- Л., 1948; [9] Скрыпник И. В., Нелинейные эллиптические уравнения высшего порядка, К., 1973; [10] Гельфанд И. М., Минлос Р. А., Шапиро З. Я., Представления группы вращений и группы Лоренца, их применения, М., 1958; [11] Схоутен Я.-А., Тензорный анализ для физиков, пер. с англ., М., 1965; [12] Лионе Ж. П., Некоторые методы решения нелинейных краевых задач, пер. с франц., М., 1972; [13] Рождественский Б. Л., Яненко Н. Н., Системы квазилинейных уравнений и их приложения к газовой динамике, М., 1968.

М. И. Войцеховский, А. И. Штерн.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.