ДИФФЕРЕНЦИАЛЬНЫЙ ИНВАРИАНТ

ДИФФЕРЕНЦИАЛЬНЫЙ ИНВАРИАНТ - выражение, составленное из одной или нескольких функций, их частных производных по независимым переменным различных порядков, а иногда и дифференциалов этих переменных, инвариантных относительно того или иного преобразования.

Пусть в дифференцируемом многообразии X_n, элементом к-рого является точка (u¹, u², ..., uⁿ), задан геометрический объект Ω (см. Геометрических объектов теория). Геометрии, объект ω того же многообразия наз. дифференциальным инвариантом порядка r относительно объекта Ω, если его координаты ω_A, A = 1, 2, ..., N, являются функциями координат Ω_α, α = 1, 2, ..., М, объекта Ω и их частных производных по координатам uⁱ, i = 1, 2, ..., n, до порядка r:

ω_A = f_A(Ω_α, ∂_iΩ_α, ..., ∂^r_i1i2...irΩ_α)

и обладают следующим свойством инвариантности относительно нек-рого преобразования координат. Именно, при замене координат

uⁱ = uⁱ(u¹', u²', ..., uⁿ')

новые координаты ω'_A объекта ω выражаются через

новые координаты Ω'_A объекта Ω и их частные производные по новым координатам - теми же самыми функциями f_A:

ω'_A = f_A(Ω'_A, ∂_iΩ_α, ..., ∂^r_i'1i'2...i'nΩ_α).

Пусть, напр., Ω - объект линейной аффинной связности (без кручения). Объект ω (тензор кривизны):

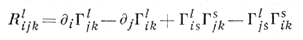
есть тензорный Д. и. порядка 1 относительно Кристоффеля символов Г^k_ij.

Пусть в Х_n задана группа (псевдогруппа) G точечных преобразований

uⁱ = fⁱ(u̅¹, u̅², ..., u̅ⁿ) (1)

и M_h - подмногообразие X_n размерности h:

uⁱ = φⁱ(t¹, t², tⁿ), (2)

параметры к-рого подвергаются преобразованиям бесконечной группы G_∞:

t^α = ψ^α(t̅^1*, t̅^2*, ..., t̅^n*).

Геометрическим дифференциальным инвариантом порядка r многообразия M_h относительно группы (псевдогруппы) G наз. функцию координат uⁱ точки М_h и их частных производных до порядка r по параметрам t^α:

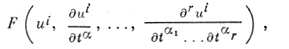
(3)

обладающую свойством инвариантности относительно преобразований (1) и (2). Именно, если в (3) заменить uⁱ по формулам (1), а частные производные от uⁱ по t^α - их выражениями через частные производные от uⁱ по t̅^α*, то получается та же функция F от u̅ⁱ и их производных по t̅^α*:

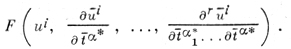
Если координаты uⁱ однородны, то функция F должна быть также инвариантна относительно преобразований

u^*i = λ(t¹, ..., tⁿ) uⁱ, λ ≠ 0,

В определении геометрич. Д. и. функцию F можно заменить геометрич. объектом. Если этот объект - ковариантный (контравариантный) вектор, то его наз. ковариантом (контравариантом).

Если инвариантно обращение в нуль нек-рого объекта, то его наз. относительным дифференциальным инвариантом.

Лит.: [1] Thomas Т. Y., The differential invariants of generalized spaces, Camb., 1934; [2] Weitzenböch R., Jnvarianten-theorie, Groningen, 1923.

В. И. Шуликовский.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.