ДИФФЕРЕНЦИАЛЬНЫЕ ИГРЫ

ДИФФЕРЕНЦИАЛЬНЫЕ ИГРЫ - раздел математич. теории управления (см. Автоматического управления теория), в к-ром изучается управление в конфликтных ситуациях. Теория Д. и. примыкает также к общей игр теории. Первые работы по теории Д. и. появились в сер. 50-х гг. 20 в.

Постановка задач теории дифференциальных игр. Различают Д. и. двух игроков и нескольких игроков. Основные результаты получены для задач с двумя игроками. Содержательное описание этих задач укладывается в следующую схему. Имеется динамическая система, в к-рой часть управляющих воздействий подчинена игроку I, а другая часть - игроку II. При постановке задачи, стоящей перед игроком I или II, предполагается, что выбор управлений этого игрока, гарантирующий ему достижение определенной цели при любом неизвестном заранее управлении противника, может опираться лишь на нек-рую информацию о текущих состояниях системы. В теории Д. и. рассматриваются также задачи управления в условиях неопределенности, когда помехи, действующие на систему, трактуются как управления противника. Напр., постановка задачи игрока I описывается следующим образом. Обычно предполагается, что движение управляемой системы задается дифференциальным уравнением

ẋ' = f(t, х, u, v), (1)

где х - фазовый вектор системы, u и v - управляющие векторы игроков I и II соответственно. Определен класс стратегий U игрока I, и для каждой стратегии U ∈ U определен пучок движений X(U), к-рый порожден этой стратегией в паре со всевозможными управлениями противника и выходит из начального состояния системы (1). Эти понятия выбираются так, чтобы они соответствовали заданным ограничениям на управления игроков и характеру информации о текущих состояниях системы, предоставленной игроку I. На движениях x(t), t ≥ t₀, системы (1) задан функционал γ(х(⋅)) (плата игры), значение к-рого игрок I стремится минимизировать (иногда функционал у зависит также от реализаций u(t), v(t), t ≥ t₀, управлений игроков). Учитывая самую неблагоприятную реализацию движения x(⋅) ∈ X(U), выбор к-рой в этой задаче предоставляется противнику, качество стратегий U ∈ U оценивается величиной

ϰ₁(U) = sup {γ(x(⋅)): x(⋅) ∈ X(U)}.

Задача игрока I состоит в определении стратегии U₀ ∈ U, на к-рой достигается минимум функционала (эта задача наз. задачей степени). Иногда рассматривается так наз. задача качества, в к-рой требуется определить условия существования стратегии U_c ∈ U, удовлетворяющей неравенству ϰ₁(U_c) ≤ с, где с - нек-рое заданное число.

Аналогичным образом формулируются задачи игрока II, к-рый максимизирует плату игры. Стратегии игрока II V ∈ V оцениваются величиной

ϰ₂(V) = inf{γ(x(⋅)): x(⋅) ∈ X(V)}.

Задача степени здесь состоит в выборе стратегии V₀ ∈ V максимизирующей значение функционала х2, а задача качества - в определении условий, при к-рых ϰ₂(V_c) ≥ с для нек-рой стратегии V_c ∈ V.

Если в задачах игроков I и II классы стратегий U и V таковы, что для всякой пары (U, V) ∈ U × V можно определить хотя бы одно движение

x(⋅) ∈ X(U) ∩ X(V),

порожденное этой парой, то говорят, что эти две задачи составляют дифференциальную игру, определенную на классе стратегий U × V. Если в Д. и. выполняется равенство

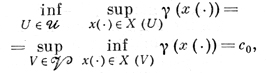
то величина c₀ наз. ценой дифференциальной игры.

Типичным примером Д. и. является игра преследования - уклонения. В этой игре х = (x₁, ..., x_k+l) = (у₁, ..., y_k, z₁, ..., z_l), где у и z -фазовые векторы преследователя и преследуемого соответственно, движение к-рых описывается уравнениями

ẏ = g (t, y, u), ż = h(t, z, v).

Наиболее часто рассматривается случай, когда выбор управлений стеснен ограничениями вида

u ∈ Р, v ∈ Q, (2)

где Р и Q - некоторые компакты. Платой в этой игре является время до встречи, т. е.

γ(x(⋅)) = T(x(⋅)) = inf {t-t₀: ||{y(t)}_m - {z(t)_m|| ≤ ε},

где {у}_m и {z}_m - векторы, составленные из первых m компонент векторов у и z. Таким образом, сближение точек {y(t)}_m и {z(t}_m нa заданное расстояние ε трактуется как встреча объектов. В случае, когда игроки располагают информацией о текущей позиции игры (t, x(t)), т. е. в позиционной игре преследования-уклонения, существует цена игры.

Формализации дифференциальных игр. Для математич. формализации Д. и. необходимы строгие определения перечисленных выше понятий. Основное внимание в теории Д. и. было уделено задачам, в к-рых игрокам известна позиция игры, а управления удовлетворяют ограничениям (2). В этом случае естественно было определить стратегии игроков как функции u = u(t, х), v = v(t, х) со значениями в компактах Р и Q соответственно. Оказалось, однако, что при таком подходе нередки случаи, когда приходится рассматривать разрывные стратегии, а порожденные ими движения нельзя определить известными в теории дифференциальных уравнений понятиями. Трудности, возникшие сначала на этом пути, привели к созданию иных постановок Д. и. Ниже рассмотрены такие формализации, где не используются позиционные стратегии. Затем дана формализация позиционных Д. и., к-рая охватывает разрывные позиционные стратегии и базируется на специальном определении движений.

Среди сложившихся направлений в теории Д. и. прежде всего следует отметить цикл исследований (см., напр., [2] - [4]), восходящих к работе У. Флеминга [1]. Здесь рассматривается аппроксимация Д. и. многошаговыми играми, где игроки последовательно (по шагам) выбирают свои управления на заданных промежутках времени [t_i, t_i+1), i = 0, 1, ..., N. Причем обычно выделяется игрок, выбирающий каждый раз свое управление первым и сообщающий этот выбор противнику. В зависимости от того, минимизирует или максимизирует этот игрок плату игры, различают мажорантную и минорантную многошаговые игры. Применение этого подхода сводится к доказательству теорем существования цены Д. и., определенной здесь как общее значение, к к-рому сходятся цены мажорантной и минорантной игр при измельчении разбиений [t_i, t_i+1), i = 0, 1, ..., N (увеличении числа шагов). Однако построение позиционных стратегий, не зависящих от дискретизации времени, при таком подходе, как правило, не рассматривается.

Л. С. Понтрягин предложил постановку игровых задач управления (см., напр., [5] - [8]), где допускается информационная дискриминация противника, т.е. при постановке задачи игрока I (или II) предполагается, что кроме реализовавшейся позиции игры (t, x(t)) этому игроку известно управление противника v(τ) (соответственно u(τ)), к-рое будет выбрано на промежутке [t, t + δ] (δ > 0 - малое число). При таком подходе достигается удобное описание игрового процесса, что позволяет построить строгую математич. теорию для широкого круга задач конфликтного управления. Однако введение информационной дискриминации дает одному из игроков I информационное превосходство над противником и вместе с тем накладывает ограничения на поведение противника, в частности не позволяет ему формировать управление по принципу обратной связи v[t] = v(t, x(t))

(соответственно u[t] = u(t, x(t))). При переходе к содержательной трактовке результатов, полученных в условиях дискриминации противника, вместо информации об управлении противника, к-рое будет выбрано им на промежутке [t, t + δ), можно использовать информацию об управлении, реализованном на промежутке [t - δ, t). Такую замену нетрудно обосновать для систем, где

f(t, х, u, v) = f₁(t, х, u) + f₂(t, х, v).

Содержательное использование глубоких теоретич. результатов, полученных в условиях дискриминации противника, достигается при рассмотрении позиционных Д. и. (см. ниже описание процедуры управления с поводырем).

Формализация позиционных Д. и. разработана Н. Н. Красовским и его сотрудниками (см., напр., [9]). Здесь рассматриваются позиционные стратегии U и V - функции u = u(t, х) и v = v(t, х), значения к-рых содержатся в компактах Р и Q соответственно. Относительно этих функций не предполагается к.-л. условий непрерывности. Движения x(t, t₀, х₀, U)(t ≥ t₀, x(t₀) = x₀), порожденные стратегией U ÷ u(t, х) игрока I, определяются как равномерные на любом отрезке [t₀, T] пределы последовательностей

аппроксимационных движений х_k(t), k = 1, 2, ..., абсолютно непрерывных функций, удовлетворяющих уравнению

ẋ_k(t) = f(t, x_k(t), u_k[t), v_k[t]), (3)

где v_k[t] ∈ Q(t ≥ t₀) - произвольные измеримые функции,

u_k[t] = u(t^(k)_i, x_k(t^(k)_i)), t^(k)_i ≤ t < t^(k)_i+1, i = 0, 1, ...,

причем

sup_i (t^(k)_i+1 - t^(k)_i) → 0 при k → ∞.

Аналогичным образом вводятся движения x(t, t₀, х₀, V), t ≥ t₀, x(t₀) = x₀. При таком определении стратегий и движений справедливо следующее положение.

Альтернатива 1. Пусть для любых векторов (t, x) ∈ ℝⁿ⁺¹ и s ∈ ℝⁿ справедливо равенство

min_u∈P max_v∈Q s'f(t, x, u, v) = max_v∈Q min_u∈P s'f(t, x, u, v), (4)

где s'f - скалярное произведение векторов s и f. Тогда, каковы бы ни были замкнутые множества M_c ⊂ ℝⁿ и N_c ⊂ ℝⁿ⁺¹, начальная позиция (f₀, х₀) и момент ϑ ≥ t₀ всегда либо существует стратегия U_* такая, что для любого движения x(t) = x(t, t₀, х₀, U_*) точка (t, x(t)) попадет на М_c к моменту t = ϑ, оставаясь в N_c вплоть до ее встречи с М_c; либо существует стратегия V_*, к-рая для любого движения x(t) = x(t, t₀, x₀, V_*) гарантирует или уклонение точки (t, x(t)) от попадания на М_c при t₀ ≤ t ≤ ϑ, или нарушение фазового ограничения (t, x(t)) ∈ N_c раньше, чем точка (t, x(t)) попадет на М_c.

К решению такой игры сближения-уклонения сводится исследование многих типов Д. и., для к-рых из альтернативы 1 следует существование цены игры. При постановке позиционных Д. и. возможны и другие определения стратегий и движений. Напр., при рассмотрении разрывных стратегий иногда удобно либо заменять разрывную правую часть дифференциального уравнения неоднозначной и использовать аппарат теории дифференциальных уравнений в контингенциях, либо аппроксимировать разрывные стратегии непрерывными (см., напр., [10]). Однако такие подходы могут оказаться неудачными. Известны примеры, в к-рых оптимальное решение Д. и., полученное в рамках описанной здесь формализации, не удается достичь и даже аппроксимировать в рамках других формализации, опирающихся на уравнения в контингенциях или непрерывные стратегии.

Если условие (4) нарушается, то различают постановку Д. и. в классе стратегий одного и контрстратегий другого игроков, к-рой отвечает детерминированное решение Д. и., и постановку Д. и. в классе смешанных стратегий обоих игроков, содержание к-рой раскрывается при аппроксимации смешанных стратегий соответствующими стохастическими процедурами управления. Контрстратегии U_v, V_u отождествляются с функциями u = u(t, х, v) ∈ P, v = v(t, х, u) ∈ Q, борелевскими по переменным v, и соответственно. Движения x(t, t₀, х₀, U_v), t ≥ t₀, x(t₀) = x₀, определяются как пределы аппроксимационных движений x_k(t) (3), где

v_k[t] = u(t^(k)_i, x_k(t^(k)_i), v_k[t]), t^(k)_i ≤ t < t^(k)_i+1, i = 0, 1, ... .

Аналогично определяются движения x(t, t₀, х₀, V_u). Смешанные стратегии U, V отождествляются с функциями μ = μ(t, х), ν = ν(t, х), значениями к-рых являются вероятностные меры, заданные на компактах Р, Q соответственно. Движения x(t, t₀, х₀, Ũ), t ≥ t₀, x(t₀) = x₀, определяются как пределы аппроксимационных движений x^t), t^t0, удовлетворяющих уравнению

ẋ_k(t) = ∫_P∫_Q f(t, x_k(t), u, v) dμ_k[t] dν_k[t],

где

μ_k = μ(t^(k)_i, x_k(t^(k)_i)), t^(k)_i ≤ t < t^(k)_i+1. i = 0, 1, ...,

ν_k[t] - некоторая слабо измеримая функция. Аналогичным образом вводятся движения x(t, t₀, х₀, Ṽ).

Для Д. и. сближения-уклонения всегда справедлива альтернатива 2 (альтернатива 3), формулировка к-рой получается из формулировки альтернативы 1 заменой стратегии одного из игроков на соответствующую контрстратегию (соответственно, заменой стратегий U_* и V_* смешанными стратегиями Ũ_* и Ṽ_*). Для Д. н., сводящихся к игре сближения-уклонения и рассматриваемых в классе позиционных стратегий одного из игроков и контрстратегий противника (в классе смешанных стратегий {Ũ} и {Ṽ}), устанавливается существование цены Д. и., причем здесь не предполагается условие (4). Решения Д. и. в указанных классах стратегий могут оказаться неустойчивыми по отношению к информационным помехам. Для стабилизации этих решений вводится процедура управления с поводырем (см. [9]). Здесь наряду с реальной системой рассматривается эталонная система - поводырь, движение к-рой моделируется в вычислительной машине и известно с любой требуемой точностью. Управление игрока в реальной системе и движение поводыря формируются так, чтобы движения исходной и моделируемой систем взаимно отслеживались, причем поводырь сохраняется на нек-ром мосту, соединяющем начальную позицию с целевым множеством. Такая процедура управления оказывается устойчивой к ошибкам измерения и помехам, действующим на систему. При моделировании движения поводыря можно использовать конструкции, допускающие дискриминацию противника.

Методы теории дифференциальных игр. Один из методов решения Д. и. был предложен Р. Айзексом [11]. Этот подход примыкает к методу динамического программирования и основан на интегрировании специального уравнения с частными производными, решение к-рого определяет цену игры c₀(t, х) как функцию исходной позиции игры. Оптимальные стратегии игрока I (или II) выбираются здесь так, чтобы обеспечить невозрастание (неубывание) цены игры вдоль порожденных ими движений системы. Однако нередки случаи, когда цена игры является разрывной функцией позиции игры, поэтому применение данного подхода требует специального анализа решений вблизи поверхностей разрыва функции c₀(t, х) или ее частных производных. Полное исследование сингулярностей и обоснование этого метода оказываются весьма сложными и их удается осуществить лишь в немногих примерах.

Наиболее полно изучены линейные Д. п., т. е. случай, когда

f(t, х, u, v) = A(t)х + В(t)u + С(t)v,

где А, В, С - непрерывные матрицы соответствующих размерностей. Для линейных задач преследования и уклонения Н. Н. Красовский сформулировал правило экстремального прицеливания (см., напр., [12]), к-рое позволило решить эти задачи (без дискриминации противника) при условии регулярности и, в частности, в случае однотипных объектов. Элементы этого решения описываются следующим образом. Пусть W(t_*, ϑ, G) - множество программного поглощения, т. е. совокупность точек x_* ∈ ℝⁿ, для к-рых для всякого управления

v(t) ∈ Q существует управление u(t) ∈ P, t_* ≤ t ≤ ϑ, такое, что пара этих управлений переводит систему из состояния x(t_*) = x_* на множество G ⊂ ℝⁿ в момент времени f = ϑ. Вводится функция

ε₀(t, х, ϑ) = inf {ε: x ∈ W(t, ϑ, M_ε)},

где M_ε - евклидова ε-окрестность целевого множества М. В области Г_ϑ = {(t, х) : ε₀(t, х, ϑ) > 0} величина ε₀(t, х, ϑ) определяется соотношением

ε₀(t, х, ϑ, ) = max_l ϰ(l, t, x, ϑ), l ∈ ℝⁿ, ||l|| ≤ 1, (5)

где для функции ϰl известно простое выражение через опорные функции множеств Р, Q и выпуклого множества М (см. [12]). При условии выпуклости функции ϰ по переменной l (сильное условие регулярности) в области Г_ϑ максимум в (5) достигается на единственном векторе l₀(t, х, ϑ), к-рый выбирается в качестве краевого условия в принципе максимума, определяющем выбор экстремального управления u₀. Построенная таким образом стратегия U₀ ĕ u₀(t, х) обеспечивает встречу с множеством М к моменту t = ϑ из любой позиции (t₀, х₀), где ε₀(t₀, х₀, ϑ) = 0. [Указанные построения опираются лишь на информацию о позиции игры и эффективно реализуются на ЭВМ.] Решение задачи сближения с помощью программной конструкции можно получить и при ослабленных условиях регулярности.

Исследование линейных задач преследования при различных предположениях регулярности проводилось Е. Ф. Мищенко, Л. С. Понтрягиным, Б. Н. Пшеничным (см., напр., [13], [14], в частности, описано [13] решение линейной задачи преследования при так наз. условиях локальной выпуклости, при к-рых имеет место указанное выше сильное условие регулярности).

Одним из наиболее удобных способов решения игровых задач управления является прямой метод. В тех задачах, где возможно применение этого метода, управление игрока выбирается так, чтобы при любом противодействии противника осуществлялось отслеживание нек-рого вспомогательного процесса, приводящее к успешному окончанию игры. В случае однотипных объектов (С = -В, Q = λP, λ ≤ 1) и при условии дискриминации противника прямой метод решения задачи преследования назначает выбор управления игрока I в виде суммы двух слагаемых, одно из к-рых копирует управление противника, а другое совпадает с решением программной задачи на быстродействие перевода системы

х̇ = A(t)х + В(t)w, w ∈ (1 - λ)P,

на целевое множество М. Впервые прямой метод был описан Л. С. Понтрягиным [5] для линейной задачи преследования. Позднее были указаны условия, при к-рых прямой метод дает оптимальный результат [15]. Затем прямой метод был развит для решения нелинейных задач и для задан с интегральными ограничениями (см., напр., [16], [17]). Во всех этих исследованиях прямой метод использовался при условии дискриминации противника; он был развит также и для решения позиционных игр (см., напр., [9]).

Задача об убегании. В этой задаче требуется определить условия, при к-рых преследуемый объект может обеспечить уклонение от встречи с преследователем при всех t ≥ t₀. Исследование этого вопроса было начато Л. С. Понтрягиным и Е. Ф. Мищенко (см. [7], [8]), к-рые указали условия разрешимости линейной задачи об убегании и полупили оценку гарантируемого расстояния между преследующей и преследуемой точками. Подход, предложенный ими, был обобщен затем для исследования других случаев задачи об убегании.

Предложенное Л. С. Понтрягиным [6] понятие альтернированного интеграла позволило описать структуру множества начальных позиций, из к-рых возможно окончание линейной игры преследования в заданный момент времени t = ϑ. Альтернированный интеграл определяется как предел рекуррентной процедуры, в к-рой исходное множество А₀ совпадает с целевым множеством M ⊂ ℝⁿ, а каждое последующее множество A_i+1 определяется по предыдущему операцией программного поглощения, т. е. A_i+1 = W(τ_i+1, τ_i, A_i), где τ_i+1 = τ_i - Δ, τ₀ = ϑ, Δ > 0 - шаг рекуррентной процедуры. Б. Н. Пшеничный [18] при исследовании структуры Д. и. преследования в качестве элементарной операции также использовал программное поглощение, где в отличие от предыдущего случая требовалось лишь, чтобы продолжительность перехода из точек x ∈ A_i+1 на А_i не превосходила числа Δ, но, вообще говоря, не равнялась этому числу. Такая рекуррентная процедура позволила в общем случае нелинейной системы описать структуру множества позиций, из к-рых игру преследования можно окончить к заданному моменту времени.

Была также предложена экстремальная конструкция для решения позиционных Д. и. (см., напр., [9]). Этот подход используется как для решения конкретных примеров, так и при доказательстве общих положений, в частности альтернатив 1-3, указанных выше. Напр., при решении задачи сближения с M_c ⊂ ℝⁿ⁺¹ в классе стратегий U ĕ u(t, х) при условии (4), согласно экстремальной конструкции, в пространстве позиций выделяется множество W_u ⊂ ℝⁿ⁺¹, образующее мост, к-рый соединяет начальную позицию с целевым множеством М_c и лежит целиком во множестве N_c. Мост обладает так наз. свойством u-стабильности, т. е. для любых (t_*, x_*) ∈ W_n, v_* ∈ Q и t^* ≥ t_* существует решение x(t) уравнения в контингенциях

ẋ(t) ∈ ω{f(t, x(t), u, v_*): u ∈ P),

х(t_*) = х_*,

для к-рого либо (t^*, x(t^*)) ∈ W_u, либо (τ, х(τ)) ∈ М_c при нек-ром τ ∈ [t_*, t^*]. Вводится экстремальная к мосту W_u стратегия U^(e) ĕ u^(e)(t, х), определяемая соотношением

min_u∈P max_v∈Q (х - w)' f(t, x, u, v) = max_v∈Q (x - w)' f(t, x, u^(e)(t, x), v),

где w - вектор, для к-рого (t, w) - точка множества W_u, ближайшая к позиции (t, х). Экстремальная стратегия удерживает движения на мосту W_u и тем самым доставляет решение задачи о сближении.

В этой конструкции основным моментом является определение подходящих стабильных мостов, после чего построение экстремальных стратегий не доставляет больших трудностей. Использование известных рекуррентных процедур для определения таких мостов ограничивается значительными трудностями вычислительного характера, поэтому важным является исследование эффективных способов построения стабильных мостов. Один из таких способов доставляет прямой метод. Другой способ - построение стабильных мостов в форме множеств регулярного программного поглощения. В нелинейном случае программное поглощение определяется с помощью специальных программных управлений-мер (см., напр., [9]). В регулярных случаях программного поглощения решение задач конфликтного управления можно довести до алгоритмов, реализуемых на ЭВМ.

Основные направления исследований дифференциальных игр. Изложенные выше результаты относились в основном к Д. и., в к-рых движение описывается обыкновенным дифференциальным уравнением (1), где управляющие векторы удовлетворяют ограничениям (2). Аналогичные результаты получены для игровых задач управления, в к-рых движение описывается дифференциальными уравнениями с отклоняющимся аргументом, а также для задан с интегральными ограничениями на управления игроков (см., напр., [17]).

Для исследования структуры Д. и. представляет интерес изучение задач конфликтного управления, где движение задается обобщенной динамич. системой (см., напр., [19], [20]). Рассмотрено решение Д. и. в классе квазистратегий, к-рые формируют управление игрока по реализовавшемуся управлению противника; предложены также итерационные процедуры для определения функции цены и стабильных мостов (см., напр., [21]).

Кроме Д. и. с двумя игроками, рассматриваются также Д. и. N лиц. Постановка Д. и. N лиц обычно предполагает, что каждый из игроков, распоряжающийся выбором своего управления, стремится минимизировать нек-рый функционал, определенный на траекториях управляемой системы. При этом допускается использование ими лишь информации о текущих позициях игры. Задача заключается, напр., в определении условий, при к-рых в таких играх имеется точка равновесия по Нэшу в заданном классе стратегий игроков.

Важный раздел теории Д. и. составляют игровые задачи управления с неполной информацией. В этих задачах предполагается, что неполнота информации заключается либо в незнании части компонент фазового вектора x(t), либо в измерении текущей позиции игры с нек-рым запаздыванием, либо в неточном измерении положения фазовой точки x(t), причем возможен случай, когда для погрешности измерения указаны лишь допустимая область, и случай, когда задано нек-рое статистич. описание этой погрешности.

Лит.: [1] Fleming W. Н., Contributions to the theory of games», 1957, v. 3, p. 407 - 12; [2] Varaiуa P., Lin Jiguan G., «SIAM J. Contr.», 1969, v. 7, № 1, p. 141-57; [3] Пeтpов H. H., «Докл. АН СССР», 1970, т. 190, № 6, с. 1289-91; [4] Friedman A., «J. Different. equat.», 1970, v. 7, № 1, p. 111-25; [5] Понтрягин Л. С., «Докл. АН СССР», 1967, т. 174, № 6, с. 1278-80; [6] его же, там же, т. 175, № 4, с. 764-66; [7] его же, «Тр. Матем. ин-та АН СССР», 1971, т. 112, с. 30-63; [8] Понтрягин Л. С., Мищенко Е. Ф., «Дифференц. уравнения», 1971, т. 7, № 3, с. 436-45; [9] Красовский Н. Н., Субботин А. И., Позиционные дифференциальные игры, М., 1974; [10] Кротов В. Ф., Гурман В. И., Методы и задачи оптимального управления, М., 1973; [11] Айзеке Р., Дифференциальные игры, пер. с англ., М., 1967; [12] Красовский Н. Н., Игровые задачи о встрече движений, М., 1970; [13] Мищенко Е. Ф., Понтрягин Л. С., «Докл. АН СССР», 1967, т. 174, № 1, с. 27-29; [14] Пшеничный Б. Н., «Кибернетика», 1967, № 6, с. 54-64; [15] Гусятников П. Б., Никольский М. С., «Докл. АН СССР», 1969, т. 184, № 3, с. 518-21; [16] Чикрий А. А., сб. «Теория оптимальных решений. Тр. семинара», в. 3, К., 1969, с. 17-25; [17] Никольский М. С., «Дифференц. уравнения», 1972, т. 8, № 6, с. 964-71; [18] Пшеничный Б. Н., «Докл. АН СССР», 1969, т. 184, № 2, с. 285-87; [19] Nаrdzеwski С. R., «Adv. in game theory. Ann. of Math. Studies», 1964, p. 113-26; [20] Rоxin E., «J. Optimiz. theory and appl.», 1969, v. 3, № 3, p. 153-63; [21] Ченцов А. Г., «Матем. сб.», 1976, т. 99, № 3, с. 394-420.

М. С. Никольский, А. И. Субботин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.