ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ С ОСОБЕННОСТЯМИ В КОЭФФИЦИЕНТАХ

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ С ОСОБЕННОСТЯМИ В КОЭФФИЦИЕНТАХ - уравнение с частными производными, коэффициенты и свободный член к-рого на некоторых многообразиях из замыкания области их задания имеют разрывы первого рода или обращаются в бесконечность.

Типичными уравнениями такого типа являются, например, уравнение Лаврентьева-Бицадзе

sign y⋅u_xx + u_yy = 0

и уравнение Эйлера - Пуассона-Дарбу

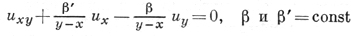
или

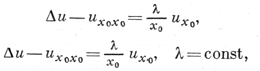
где Δ - оператор Лапласа по переменным х₁, ..., х_n.

К уравнениям с особенностями в коэффициентах относятся многие вырожденные уравнения с частными производными.

Центральное место в теории дифференциальных уравнений с особенностями в коэффициентах занимает исследование разрешимости начальных краевых и смешанных задач в их классической и обобщенной постановках, а также поиск новых корректно поставленных задач. Сравнительно полно исследованы краевые задачи для линейных эллиптич., гиперболич. и параболич. уравнений 2-го порядка со слабыми особенностями в коэффициентах, к-рые, как правило, суммируемы со степенью, большей размерности области их задания. В случае, когда коэффициенты этих уравнений претерпевают лишь разрывы первого рода на нек-рых достаточно гладких поверхностях, лежащих внутри области задания, создана весьма полная теория основных краевых задач. См. Дифференциальное уравнение с частными производными; задача с разрывными коэффициентами, а также [3], [5], [6].

Лит.: [1] Бицадзе А. В., Уравнения смешанного типа, М., 1959; [2] Векуа И. Н., Обобщенные аналитические функции, М., 1959; [3] Ладыженская О. А., Уральцева Н. Н., Линейные и квазилинейные уравнения эллиптического типа, М., 1964; [4] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [5] Олейник О. А., «Докл. АН СССР», 1959, т. 124, № 6, с. 1219-22; [6] Самарский А. А., «Докл. АН СССР», 1958, т. 121, № 2, с. 225-28.

А. М. Нахугиев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.