ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА - уравнение, к-рое содержит хотя бы одну производную 2-го порядка от неизвестной функции u(х) и не содержит производных более высокого порядка. Напр., линейное уравнение 2-го порядка имеет вид

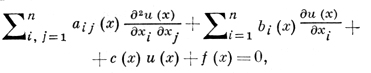
(1)

где точка х = (х₁, х₂, ..., х_n) принадлежит нек-рой

области Ω ⊂ R_n, в к-рой определены действительнозначные функции a_ij(x), b_i(x), с(х), и в каждой точке х ∈ Ω. хотя бы один из коэффициентов a_ij(x) отличен от нуля. Для любой точки x₁ ∈ Ω существует такое неособое преобразование независимых переменных ξ = ξ(x), что уравнение (1) в новых координатах ξ = (ξ₁, ξ₂, ..., ξ_n) примет вид

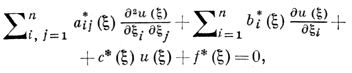
(2)

где коэффициенты а^*_ij(ξ) в точке ξ₀ = ξ(x₀) равны нулю при i ≠ j, и равны ±1 или 0 при i = j, Уравнение (2) наз. канонич. видом уравнения (1) в точке х₀.

Число к положительных и число l отрицательных в точке ξ₀ коэффициентов а^*_ij(ξ) в уравнении (2) зависит только от коэффициентов a_ij(x) уравнения (1). Это обстоятельство позволяет классифицировать дифференциальные уравнения (1) следующим образом. Если k = n или l = n, то уравнение (1) наз. эллиптическим в точке х₀; если k = n - 1, a l = 1, или k = 1, а l = n - 1, то - гиперболическим; если k + l = n и 1 < k < n-1, то - ультрагиперболическим. Уравнение наз. параболическим в широком смысле в точке х₀, если хотя бы один из коэффициентов a^*_ij(ξ) равен нулю в точке ξ₀ = ξ(х₀), k + l < n; уравнение наз. параболическим в точке х₀, если только один из коэффициентов а^*_ij(ξ) равен нулю в точке ξ₀ (пусть a^*₁₁(ξ₀) = 0), а все остальные коэффициенты a^*_ii(ξ) одного знака и коэффициент b^*₁(ξ₀) ≠ 0.

В случае двух независимых переменных (n = 2) тип уравнения удобнее определять с помощью функции

Δ(х) = а₁₁а₂₂ - а₁₂а₂₁.

Так, уравнение (1) является эллиптическим в точке x₀, если Δ(x₀) > 0; гиперболическим, если Δ(x₀) < 0, и параболическим в широком смысле, если Δ(х₀) = 0.

Уравнение наз. эллиптическим, гиперболическим и т. д. в области, если оно эллиптично, соответственно, гиперболично и т. д. в каждой точке этой области. Так, напр., уравнение Трикоми уu_xx + u_yy = 0 эллиптично при y > 0, гиперболично при y < 0 и параболично в широком смысле при у = 0.

Преобразование переменных ξ = ξ(x), к-рое приводит уравнение (1) к канонич. виду в точке х₀, зависит от этой точки. В случае трех и более независимых переменных, вообще говоря, не существует неособого преобразования, приводящего уравнение (1) к канонич. виду одновременно во всех точках нек-рой окрестности точки х₀, т. е. к виду

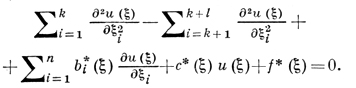
В случае же двух независимых переменных (n = 2) такое приведение уравнения (1) к канонич. виду возможно при нек-рых условиях на коэффициенты а_ij(х); напр., если функции a_ij(x) непрерывно дифференцируемы до 2-го порядка включительно и уравнение (1) одного типа в нек-рой окрестности точки х₀. Пусть

Ф(х, u, u_x1, ..., u_xn, u_x1x1, u_x1x2, ..., u_xnxn) = 0 (3) - нелинейное уравнение 2-го порядка, где u_xi = ∂u(x)/∂x_i, u_xixj = ∂²u(x)/∂x_i∂x_j и пусть в каждой точке из области определения действительнозначной функции Ф существуют производные ∂Ф/∂u_xixj и выполнено условие

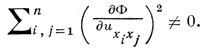
Для классификации нелинейных уравнений вида (3) фиксируют некоторое решение u*(х) этого уравнения и рассматривают линейное уравнение

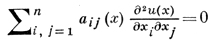
(4)

с коэффициентами

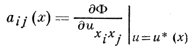
Уравнение (3) для данного решения u*(х) наз. эллиптическим, гиперболическим и т. д. в точке х₀ (или в области), если эллиптично, гиперболично и т. д. в этой точке (соответственно в области) уравнение (4).

К решению дифференциальных уравнений 2-го порядка сводится весьма широкий класс физических задач. См., напр., Волновое уравнение, Телеграфное уравнение, Теплопроводности уравнение, Лапласа уравнение, Пуассона уравнение, Гельмгольца уравнение, Трикоми уравнение.

А. К. Гущин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.