ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; функциональные методы решения

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; функциональные методы решения - методы, основанные на рассмотрении левой части уравнения как оператора, действующего в функциональном пространстве, определенном соответствующим образом. Наибольшее развитие функциональные методы получили в применении к линейным уравнениям с частными производными. В этом случае функциональные методы условно могут быть разбиты на две группы: а) относящиеся к спектральной теории дифференциальных операторов и б) используемые прн выяснении общего характера разрешимости уравнений, краевых задач и свойств решений. Внутри группы б) удобно, в свою очередь, выделить, с одной стороны, методы, опирающиеся лишь на общие теоремы функционального анализа (теории операторов), а с другой - методы, существенно использующие технику преобразования Фурье. Для первых характерно непосредственное рассмотрение краевых задач для общих уравнений с переменными коэффициентами; для вторых отправной точкой является изучение дифференциального оператора с постоянными коэффициентами, часто безотносительно к краевым условиям, а переход к переменным коэффициентам (когда это возможно) осуществляется при помощи соответствующей «теории возмущений». Получаемые в обоих направлениях результаты дополняют друг друга.

Функциональные методы возникли при использовании связи между задачей минимизации функционала

J(u) = ∫_V {(∂u/∂x)² + (∂u/∂y)² - 2fu} dv (1)

в классе действительных функций u(х, у), удовлетворяющих на границе S области V (для простоты - двумерной) условию

u|_S = 0, (2)

и задачей решения уравнения Пуассона

-Δu = f (3)

в V [являющегося уравнением Эйлера для (1)] при тех же краевых условиях (2). Если f не является гладкой (напр., f ∈ H(V) - гильбертову пространству функций с суммируемым в V квадратом), то минимум для (1) достигается на функциях, не имеющих, вообще говоря, вторых производных, входящих в уравнение (3), т. е. эти функции дают лишь обобщенное решение задачи (3), (2). Для исчерпывающего описания возникающей ситуации (см. [1], [2]) вводится гильбертово пространство W¹, получаемое пополнением линейного многообразия гладких функций, удовлетворяющих (2), в норме, порождаемой скалярным произведением

{u, v} = ∫_V {∂u/∂x ∂v/∂x + ∂u/∂y ∂v/∂y} dV.

Тогда под решением задачи (3), (2) понимается элемент u ∈ W¹ такой, что для любого элемента v ∈ W¹ выполняется равенство

{u, v} = (f, v), (4)

где круглые скобки означают скалярное произведение в H(V). Минимум для (1) при любой f ∈ H также достигается в W¹ и дает решение задачи (3), (2) в смысле (4), являющееся единственным. Всякое классическое (имеющее вторые производные) решение задачи (3),

(2) удовлетворяет равенству (4) при любой допустимой функции v и, значит, является обобщенным. Отсюда, в частности, следует определение, с помощью обобщенного решения, нек-рого расширения классич. оператора -Δ, заданного первоначально на гладких функциях, удовлетворяющих условию (2). Вопрос «при каких условиях на f и границу S обобщенное решение будет классическим?» значительно более сложен (это -вопрос о так наз. дифференциальных свойствах обобщенного решения).

В рассмотренной схеме существование обобщенного решения следовало из существования в W¹ элемента, реализующего минимум функционала (1). В дальнейшем было замечено, что теорема существования может быть получена непосредственно из определения (4) при помощи так наз. теоремы Рисса об общем виде линейного ограниченного функционала (см. [1]). Последующее развитие теории идет в нескольких направлениях. Приведенные построения немедленно обобщаются на случай, когда -Δ заменяется на общий самосопряженный положительный эллиптич. оператор порядка 2m с переменными коэффициентами. При этом, естественно, в скалярное произведение будут входить производные порядка m. Свойство полной непрерывности обратного оператора позволяет установить характер спектра соответствующих задач и установить справедливость для них Фредгольма альтернативы. Можно получить теорему существования решения и в случае, когда в уравнении присутствует подчиненный главной эллиптич. части кососимметрич. оператор

(напр., вместе с -Δ имеются члены а(х, у) ∂u/∂x + b(x, y)∂u/∂y), т. е. и при отсутствии связи с вариационными задачами [3].

Обобщения иного характера возникают из замечания о сохранении теоремы существования и единственности обобщенного решения задачи (3), (2) и в том случае, когда f - произвольный ограниченный линейный функционал над W¹. Пространство всех таких функционалов может быть получено пополнением Н по новой норме

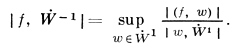
(5)

Получаемое пространство W^-1 оказывается существенно шире Н. Напр., в одномерном случае (V - интервал (-1, 1)) последовательность функций

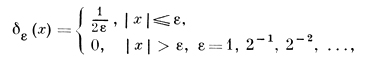
сходится в W^-1, но расходится в Н. Предел этой последовательности не является функцией в обычном смысле, т. е. пространство W^-1 содержит обобщенные функции. В то же время неравенство

|〈f, w〉| ≤ |f, W^-1||w, W¹|

(скобки 〈 , 〉 обозначают действие функционала f на элемент w ∈ W¹) обеспечивает справедливость теоремы существования и единственности в случае f ∈ W^-1. Этот результат интересен еще и в том отношении, что теперь оператор -Δ устанавливает изоморфизм между пространствами W¹ и W^-1. При f ∈ H и гладкой S обобщенное решение задачи (3), (2) не только принадлежит W¹, но всегда имеет и вторые обобщенные производные (u ∈ W²), причем

|u, W²| ≤ c|f, Н|.

При n = 2 (n - размерность V) пространство W^-2 (функционалов над W²) содержит δ-функцию, т. е. функционал, определяемый равенством 〈δ_x0, u〉 = u(х₀). Существует принадлежащее пространству Н обобщенное решение уравнения

-Δv_x0 = δ_x0

такое, что для u-обобщенного решения задачи (3), (2) верна формула

(-Δu, v_x0) = 〈u, -Δv_x0〉 = 〈u, δ_x0〉 = u(х₀),

или

u(x₀) = (f, v_x0).

Это составляет абстрактную теорему существования функции Грина задачи (3), (2). Соответствующие построения осуществимы и в пространстве произвольного числа измерений для общих эллиптич. операторов [4].

Следующим (после эллиптич. операторов) объектом, к к-рому успешно были применены общие функциональные методы, явились уравнения с выделенным переменным - «временем», непосредственно обобщающие классияеские параболич. и гиперболич. уравнения математич. физики. Здесь основные результаты условно могут быть разбиты на 3 группы: относящиеся к операторным уравнениям с 1-й и 2-й производной по времени [5], к симметричным положительным системам с частными производными 1-го порядка [3], [6] и к задаче Коши для гиперболич. уравнения произвольного порядка. Первая группа результатов излагается обычно либо в контексте обыкновенных дифференциальных уравнений в банаховом пространстве и теории полугрупп операторов, либо, вместе со второй и третьей группами, в рамках так наз. техники энергетич. неравенств. Последняя, в общих чертах, заключается в следующем. Для гладких решений уравнения со временем, записанного в операторной форме

Lu = f, (6)

подчиненных соответствующим начальным и краевым условиям, устанавливается неравенство вида

|u, Н₁| ≤ c|Lu, Н₂|, (7)

где H₁, Н₂ - соответствующим образом определенные функциональные пространства. Для простоты их считают гильбертовыми. Напр., для u ∈ С², удовлетворяющих в единичном квадрате V уравнению

Lu ≡ ∂²u/∂t² - ∂²u/∂x² = f

и условиям

u|_t=0 = u'_t|_t=0 = u|_x=0 = u|_x=1 = 0,

умножением на ∂u/∂ интегрированием по V и элементарными преобразованиями можно получить неравенство вида

∫_t=T[(∂u/∂x)² + (∂u/∂t)²] dx ≤ 4∫_V f² dx dt, 0 ≤ T ≤ 1, (8)

(являющееся математич. выражением нек-рого закона сохранения, откуда и термин «энергетическое неравенство»), соответствующее неравенству (7) при надлежащем определении норм в Н₁, H₂. Определив обобщенное решение уравнения (6) как элемент u ∈ H₁, для к-рого существует последовательность гладких функций u_i, удовлетворяющих описанным краевым условиям, такая, что u_i → u в Н₁ и Lu_i → f в Н₂, одновременно получают определение оператора L: Н₁ → Н₂ (снова являющегося расширением классического), для к-рого существует ограниченный обратный оператор, что эквивалентно теореме единственности обобщенного решения. Следующим шагом исследования уравнения (6) является доказательство существования такого решения при любой допустимой правой части f ∈ H₂. Так как область изменения R_L оператора L является замкнутым подпространством в Н₂, доказательство единственности эквивалентно доказательству пустоты ортогонального дополнения к R_L: из равенства

(Lu, v)₂ = 0 для любого u ∈ 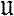_L (9)

(скалярное произведение в Н₂) следует v = 0. Равенство (9), с точки зрения теории операторов, означает, что v ∈ 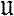_L и L*v = 0, т. е. требуемый результат немедленно следовал бы из теоремы о единственности решения уравнения L*v = g. Однако доказательство такой теоремы требует специальных построений, часто весьма сложных, поскольку для L* (определенного с точки зрения классич. анализа с помощью нек-рого интегрального тождества) наличие неравенства, аналогичного (7) (так же, как и наличие для v последовательности сходящихся к ней гладких функций, удовлетворяющих нужным граничным условиям), отнюдь не очевидно. Возникающие трудности являются отражением несамосопряженности задач со «временем». При исследовании гиперболич. уравнений 2-го и высшего порядков использование (9) для доказательства равенства v = 0 проводится обычно следующим образом: подбирается оператор Р* такой, что P*v ∈ _L и

(LP*v, v)₂ ≥ c|v, H₂|². (10)

Если заметить еще, что получение (7) основано обычно на рассмотрении выражения вида (Lu, Qu)₂, где Q -оператор, подобранный так, что

(Lu, Qu)₂ ≥ c|u, H₁|²,

и записать теперь (10) в виде

(L*v, P*v)₁ ≥ c|v, Н₂|²,

то можно считать, что исследование (6) основывается на этой паре неравенств (называемых иногда дуальными). Сказанное относится главным образом к гиперболич. уравнениям. Параболич. уравнения допускают трактовку, более близкую к эллиптич. случаю.

Преобразование Фурье позволяет провести, в известном смысле, исчерпывающее изучение задачи Коши для уравнений с постоянными коэффициентами [10]. Кроме того, преобразование Фурье, вместе с так наз. «замораживанием коэффициентов» (т. е. заменой оператора с переменными коэффициентами оператором с постоянными коэффициентами, равными значениям соответствующих коэффициентов в нек-рой фиксированной точке), часто используется для получения энергетич. неравенств при использовании схем рассмотренного выше типа, а также играет важную роль в локальной характеризации операторов и краевых условий при исследовании краевых задач для эллиптич. уравнений [10]. Дальнейшее развитие этих идей привело к введению и изучению псевдодифференциальных операторов. Кроме того, с помощью преобразования Фурье было установлено, что для дифференциальной операции L с постоянными коэффициентами, рассматриваемой в компактной области V евклидова пространства на функциях u ∈ С̇^∞(V), т. е. равных нулю на границе вместе со всеми производными, всегда имеет место неравенство

|u, H(V)| ≤ c|Lu, H(V)|. (11)

Взяв для L замыкание L̇ в Н(V) (областью определения для L считают С̇^∞(V)) и определив L как сопряженный к L̇ (в H(V)), получают, что R_L̃ = H(V). Наличие неравенства (11) для решений уравнения (6), обеспечивающее единственность решения, автоматически влечет и разрешимость при любой правой части уравнения L*v = g, содержащего сопряженный оператор. Используя теорему Банаха, можно заключить, что существует оператор L̂, L̇ ⊂ L̂ ⊂ L̃ (т. е. L̂ является расширением минимального оператора L̇ и сужением максимального L̃), такой, что R_L̂ = H(V), причем существует ограниченный (в Н) обратный оператор

L̂^-1 (см. [10]). Можно считать, что L соответствует нек-рой краевой задаче (определяется нек-рой системой условий, «сосредоточенной» на границе и находящейся «между» тождественно нулевыми условиями и полным отсутствием условий). О характере условий, определяющих оператор L̂, в общем случае известно мало.

Использование преобразования Фурье лежит также в основе исследования широкого круга вопросов теории дифференциальных операторов, связанных с изучением структуры фундаментального решения и так наз. локальных свойств решений уравнений (в отличие от исследования свойств решений краевых задач). Сюда относятся теорема о существовании фундаментального решения для общего оператора с постоянными коэффициентами, теорема о локальной (в окрестности данной точки) разрешимости уравнения с правой частью и о характере гладкости этого решения (см. [9], [11]). В связи с тем, что в случае переменных (комплексных) коэффициентов локальная разрешимость неоднородного уравнения (6) не всегда имеет место (для уравнения

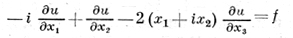
имеется такая f ∈ C^∞, что не существует решения, даже в классе обобщенных функций, ни в каком открытом непустом подмножестве R³, см. [9]), исследуются условия, обеспечивающие локальную разрешимость.

Использование функциональных методов весьма плодотворно и при изучении нелинейных уравнений с частными производными. Это прежде всего относится к вариационным методам (если вместо функционала (1) рассматривать более общий, то связанное с ним уравнение Эйлера оказывается нелинейным) (см. [12]), различным вариантам метода неподвижной точки (см. Шаудера метод), к методу продолжения по параметру (см. [3], [13]), и другим, применяемым главным образом к эллиптич. и параболич. уравнениям. Метод энергетич. неравенств успешно используется при изучении квазилинейных гиперболич. уравнений.

Лит.: [1] Соболев С. Л., Некоторые применения функционального анализа в математической физике, Новосиб., 1962; [2] Курант Р., Гильберт Д., Методы математической физики, пер. с нем., 3 изд., т. 1-2, М.-Л., 1951; [3] Берс Л., Джон Ф., Шехтер М., Уравнения с частными производными, пер. с англ., М., 1966; [4] Liоns J., Equations differentielles opérationelles et problèmes aux limites, В., 1961; [5] Xиллe Э., Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., 2 изд., М., 1962; [6] Нагумо М., Лекции по современной теории дифференциальных уравнений в частных производных, пер. с япон., М.,1967; [7] Гординг Л., Задачи Коши для гиперболических уравнений, пер. с англ., М., 1961; [8] Гельфанд И. М., Шилов Г. Е., Некоторые вопросы теории дифференциальных уравнений, М., 1958; [9] Хёрмандер Л., Линейные дифференциальные операторы с частными производными, пер. с англ., М., 1965; [10] его же, К теории общих дифференциальных операторов в частных производных, пер. с англ., М., 1959; [11] Трев Ж., Лекции по линейным уравнениям в частных производных с постоянными коэффициентами, пер. с англ., М., 1965; [12] Ладыженская О. А., Уральцева Н. Н., Линейные и квазилинейные уравнения эллиптического типа, М., 1964; [13] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957.

А. А. Дезин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.