ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; методы комплексного переменного

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; методы комплексного переменного - методы решения эллиптических Д. у. с ч. п., в к-рых используется представление решений через аналитич. функции комплексного переменного.

Теория аналитич. функций

w(z) = u(x, y) + iv(x, у)

комплексного переменного z = x + iy представляет собой теорию двух действительных функций u(х, у) и v(x, у), удовлетворяющих системе уравнений Коши - Римана: u_x - v_y = 0, u_y - v_x = 0, к-рая по существу эквивалентна уравнению Лапласа

Δu = u_xx + u_yy = 0.

Начиная с 30-х гг. 20 в. методы аналитич. функций интенсивно стали проникать в общую теорию уравнений эллиптич. типа. Это привело к созданию нового раздела анализа, существенно расширяющего рамки классич. теории аналитич. функций и ее применений. В этой области фундаментальную роль играют различные формулы представления всех решений весьма широкого класса эллиптич. уравнений через аналитич. функции одного комплексного переменного. Для линейных уравнений эти представления осуществляются с помощью нек-рых линейных операторов, выражающихся посредством коэффициентов. Эти формулы дают возможность распространить свойства аналитич. функций на решения уравнений эллиптич. типа, причем, в ряде случаев в дословной формулировке сохраняются такие важные свойства, как теорема единственности, принцип аргумента, теорема Лиувилля и др. В естественной форме обобщаются ряды Тейлора и Лорана, интегральная формула Коши, принцип компактности, принцип аналитич. продолжения и др.

Формулы комплексного представления позволяют строить разнообразные семейства частных решений уравнения, обладающие теми или иными заданными свойствами. Напр., можно строить различные классы так наз. элементарных решений, имеющих точечные особенности, к-рые используются для получения различных интегральных формул, а также так наз. полные системы частных решений; последние обладают тем свойством, что при помощи их линейных комбинаций можно приближать любые решения. Формулы комплексного представления позволяют также редуцировать широкий круг граничных задач к эквивалентным краевым задачам для аналитич. функций, а также строить эквивалентные задаче интегральные уравнения (типа Фредгольма или сингулярные). Этот метод позволяет исследовать краевые задачи нефредгольмового типа, получить условие нормальной разрешимости и явную формулу индекса. См. Краевая задача; методы комплексного переменного.

Эллиптические уравнения с аналитическими коэффициентами. Пусть дано уравнение 2-го порядка эллиптич. типа

Δu + a(x, y)∂u/∂x + b(x, y)∂u/∂y + c(x, y)u = 0, (1)

где а, b и с - аналитич. функции действительных переменных х, у в нек-рой области плоскости z = x + iy. Аналитическое продолжение коэффициентов в область независимых комплексных переменных z = x + iy, ζ = х - iy приводит уравнение (1) к виду:

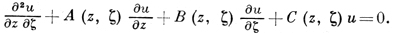
(2)

Односвязная область D₀ наз. основной областью уравнения (1), если А, В и С -- аналитич. функции двух независимых переменных в цилиндрич; области (D₀, D̅), где D₀ обозначает зеркальное изображение D₀ относительно действительной оси.

Если D ⊂ D₀ - односвязная область, то все регулярные в области D решения уравнения (1) выражаются по формуле

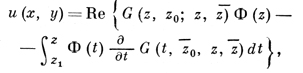
(3)

где Ф(z) - произвольная голоморфная функция в области D, z₁, z₀ ∈ D - произвольные фиксированные точки; аналитич. функция G(z, ζ, t, τ) четырех независимых комплексных аргументов в цилиндрич. области (D₀, D̅₀, D₀, D̅₀) наз. функцией Римана уравнения (1). Она является решением интегрального уравнения типа Вольтерра:

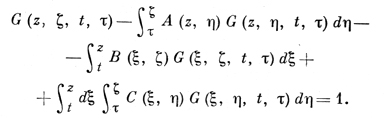
(4)

Осуществляемое формулой (3) соответствие между семейством решений {u} уравнения (1) и семейством голоморфных функций {Ф} взаимно однозначно, если зафиксировать значения мнимой части Ф в фиксированной точке z₁ области D. При z₁ = z₀ = 0 имеет место формула обращения:

Ф(z) = 2u(z/2, z/2i) = u(0, 0) G(0, 0, z, 0).

Уравнение (4) можно решить методом последовательных приближений. Таким путем можно найти приближенные выражения для функции Римана.

В случае многосвязной области D формула (3) дает, вообще говоря, многозначные решения. Чтобы получить в этом случае все однозначные решения уравнения (1), в качестве Ф в (3) надо брать многозначные функции определенного вида.

Пусть D - двухсвязная область (D ⊂ D₀), D' - ограниченный континуум, дополняющий D до односвязной области. Тогда все однозначные в области D решения уравнения (1) даются формулой

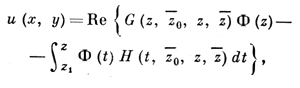
(5)

где z₁ ∈ D, z₀ ∈ D' -фиксированные точки, Ф(z) -многозначная аналитич. функция вида

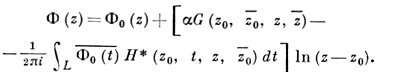
Здесь α - произвольная действительная постоянная, Ф₀(z) - произвольная голоморфная функция в области D, L - любая простая замкнутая кусочно гладкая кривая, лежащая в D и окружающая D'. Функции H и H* выражаются по формулам

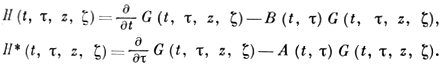
Комплексные представления вида (3) распространяются также и на системы уравнений, записываемых в векторной форме в виде (1), где u - вектор с компонентами u₁, ..., u_n, а, b, с - квадратичные матрицы порядка n, элементы которых - аналитич. функции переменных х, у.

В той области, где уравнение (1) имеет хотя бы одно положительное решение u₀ > 0, подстановкой u = u₀v его можно привести к виду

Δv + av_x + bv_y = 0

(такое решение всегда существует в малой окрестности любой фиксированной точки, а также в любой области, где с ≤ 0). В этом случае уравнение (1) эквивалентно системе уравнений, к-рая представляет собой частный случай обобщенной системы Коши - Римана вида

u_x - v_y + au + bv = 0, u_y + v_x + cu + dv = 0. (6)

Вводя в рассмотрение комплексную функцию w = u + iv, эту систему можно записать в виде

∂_z̅w + A(z)w + B(z)w̅ = 0, 2∂_z̅ = ∂_x + i∂_y (7)

Если коэффициенты А и В - аналитич. функции комплексных аргументов z и ζ (z = x + iy, ζ = x - iy) в нек-рой цилиндрич. области (D₀, D̅₀), где D₀ - односвязная область, то решение уравнения (6) в односвяз-ной области D ⊂ D₀ выражается формулой

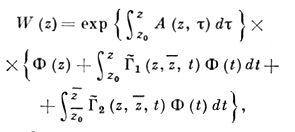
(8)

в к-poй Г̃₁ и Г̃₂ - аналитич. функции своих аргументов, выражающиеся через А и В; они строятся по методу последовательных приближений, Ф - произвольная аналитич. функция переменного z.

В случае, когда А и В - целые функции переменных х и у, представление (8) имеет место для любой односвязной области плоскости z без ограничений на поведение коэффициентов А и В вблизи бесконечности.

Пусть дано эллиптич. уравнение вида

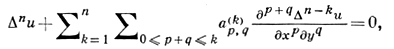
(9)

где a^(k)_p,q - аналитич. функции х, у. Если D₀ - основная область уравнения (9), то всякое регулярное решение этого уравнения в односвязной области D ⊂ D₀ выражается формулой

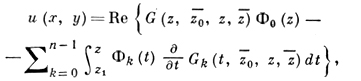
(10)

где Ф₀, ..., Ф_n-1 - произвольные голоморфные в области D функции

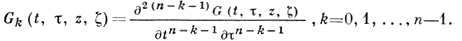
Здесь G - комплексная функция Римана уравнения (9), к-рая аналитически зависит от комплексных аргументов (t, τ, z, ζ) в цилиндрич. области (D₀, D̅₀, D₀, D̅₀). При выполнении условий

Ф_k(z₁) = Ф̅_k̅(̅z₁), k = 0, 1, ..., n-1.

формула (10) осуществляет взаимно однозначное соответствие между семейством решений {u} уравнения (9) и семейством голоморфных функций {(Ф₀, ..., Ф_n-1)}. Если D - многосвязная область, то формула (10) дает, вообще говоря, многозначные решения. По, как и в случае уравнения 2-го порядка, можно видоизменить эту формулу так, чтобы она давала все однозначные решения уравнения (9) и в многосвязной области. Формула (10) распространяется также на систему уравнений вида (9), где u - вектор, а коэффициенты - матрицы.

Для ряда уравнений математич. физики функция Римана выражается в явной форме при помощи элементарных или специальных функций.

В случае уравнения колебаний мембраны

Δu + λ²u = 0, λ = const,

G(z, ζ, t, τ) = J₀(λ√((z - t)(ζ - τ))),

где J₀ - функция Бесселя нулевого порядка; в качестве основной области можно взять всю комплексную плоскость. Случай λ = 0 дает уравнение Лапласа Δu = 0; тогда G = 1 и формула (3) принимает вид

u = Re[Ф(z)].

Для уравнения сферич. функций

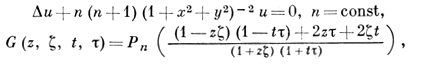
где P_n - функция Лежандра первого рода; в качестве основной области можно взять любую односвязную область D₀, для к-рой выполняется условие: если z ∈ D₀, ζ ∈ D₀, то zζ ≠ 1 (напр., круг |z| < 1). Для уравнения Эйлера - Дарбу

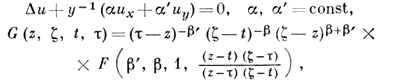
где 2β = α' + iα, 2β' = α' - iα, F - гипергеометрич. ряд, в качестве основной области можно взять полуплоскости у > 0 или y < 0. Для уравнения

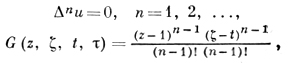
и имеет место формула Гурса

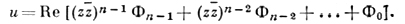
Метод комплексных представлений решений применим также к нек-рому классу нелинейных уравнений. Пусть, напр., дано известное в дифференциальной геометрии уравнение Гаусса

Δu = -2ke^u,

где k(х, у) - заданная функция. Если v₀(z) - какое-либо частное решение этого уравнения, то его же решениями являются функции вида

u(z) = v₀[Ф(z)] | Ф'(z)|²,

где Ф(z) - произвольная аналитич. функция. Если k = const, то v₀ = 4(1 - kzz̅)^-2 и все решения уравнения Гаусса выражаются формулой:

u(х, у) = 4|Ф'(z)|² (1 + k|Ф(z)|²)^-2.

Если k < 0, то надо предполагать, что |Ф(z)| < -k^-1.

Эллиптические уравнения с неаналитическими коэффициентами. Пусть дана обобщенная система уравнений Коши - Римана (7) с коэффициентами А и В, заданными на всей плоскости Е комплексного переменного z и принадлежащими классу L_p,2(Е), т. е.

А(z), B(z) ∈ L_p, |z|^-2A(1/z), |z|^-2 B(1/z) ∈ L_p, р > 2, |z| ≤ 1.

Если коэффициенты заданы в ограниченной области S и принадлежат классу L_p(S), р > 2, то они будут удовлетворять предыдущим условиям при продолжении их вне S нулем. При этих предположениях уравнение (7), вообще говоря, не имеет решения в классическом смысле. Поэтому рассматриваются так наз. обобщенные решения: функция w(z) ∈ L₁(S) наз. решением уравнения (7) в области S, если она обладает производной в смысле С. Л. Соболева ∂_ż ∈ L₁(S) и удовлетворяет уравнению почти везде в S.

Теория функций, удовлетворяющих уравнению (7), представляет собой далеко идущее обобщение классич. теории аналитич. функций (А ≡ S ≡ 0) и сохраняет существенные черты последней. Поэтому решения уравнения вида (7) наз. обобщенными аналитическими функциями.

Всякое решение уравнения (7) (в S) удовлетворяет интегральному уравнению

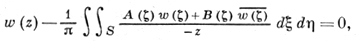
(11)

где ζ = ζ + iη, Ф(z) - голоморфная функция в S. Если Ф ∈ L_q(S̅), g > p/(p-1), p > 2, то уравнение (11) имеет единственное решение, к-рое выражается формулой вида

w(z) = Ф(z) + ∬_S Г₁(z, ζ) Ф(ζ) dξ dη + ∬_S Г₂(z, ζ) Ф̇(̇ζ̇) dξ dη (12)

Резольвенты Г₁ и Г₂ зависят от коэффициентов уравнения (7) и строятся при помощи процесса последовательных приближений.

Формула (12) дает общее (линейное) представление решений уравнения (7) через аналитич. функции Ф(z). Она, в частности, позволяет построить так наз. основные ядра

Ω₁(z, t) = X₁(z, t) + iX₂(z, t), Ω₂(z, t) - iX₂(z, t),

где t - некоторая фиксированная точка, a X₁ и X₂ -решения интегрального уравнения (11), соответствующие функциям

2Ф₁ = (t - z)^-1, 2iФ₂ = (t - z)^-1,

Эти ядра позволяют написать обобщенную формулу Коши:

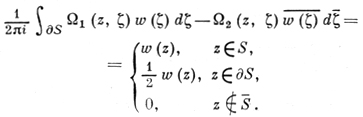
(13)

При A ≡ B ≡ 0 она обращается в классич. формулу Коши. При помощи формулы (13) на обобщенные аналитич. функции распространяются многие из тех свойств аналитич. функций, к-рые доказываются обычно с помощью формулы Коши. В частности, можно обобщить классич. теоремы об аналитич. продолжении, построить теорию обобщенных интегралов типа Коши, получить представления обобщенных аналитич. функций в виде контурных интегралов с действительной плотностью и др.

Основными ядрами сопряженного уравнения

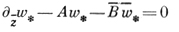
(14)

являются функции

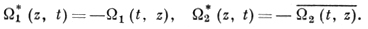
Если w и w_* удовлетворяют в S уравнениям (7) и (14), соответственно, и непрерывны в S̅, то имеет место тождество (аналог классической теоремы Коши):

Re [i∫_∂S w(z) w_*(z) dz] = 0.

Если w(z) - решение уравнения (7) в области S, то существует такая аналитическая в S функция Ф(z), что имеет место равенство

w(z) = Ф(z)e^ω(z). (15)

где

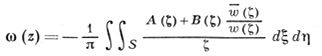
(16)

и принадлежит классу С_α(Е), α = р/(р - 2), причем ω(z) → 0, если z → ∞.

Эта формула, в частности, позволяет распространить на решения уравнений вида (7) основные теоремы классич. теории аналитич. функций: теорему единственности, теорему Лиувилля, принцип аргумента, принцип компактности и др. Формула (15) допускает обращение: задавая аналитич. функцию Ф, можно найти функцию w(z), удовлетворяющую нелинейному интегральному уравнению (15).

Пусть Ф(z) - аналитическая в области S функция, к-рая может иметь любые особенности, и t - фиксированная точка. Тогда существует решение w(z) уравнения (7) такое, что функция w₀ = w/Ф непрерывно продолжима на всю плоскость Е, принадлежит классу С_α(Е), α = (р-2)/р, не обращается в нуль нигде на плоскости Е и w₀(t) = l. Функция w₀ удовлетворяет интегральному уравнению

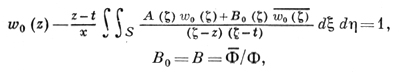
(17)

к-рое имеет единственное решение, а функция w = Ф(z)w₀ удовлетворяет нелинейному интегральному уравнению

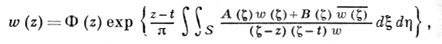
(18)

из к-рого при t → ∞ получается представление (15).

Проблема приведения эллиптич. уравнения 2-го порядка общего вида

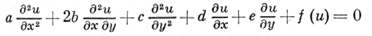
(19)

к виду (1) эквивалентна задаче редукции к канонич. виду положительной квадратичной формы

adx² + 2bdxdy + cdy², а > 0, Δ ≡ ас - b² > 0.

Последняя проблема эквивалентна отысканию гомеоморфизмов уравнения Бельтрами

∂_z̅w - q(z)∂_zw = 0, w = u + iv, (20)

где

q(z) = (a - √Δ - ib)(a + √Δ + ib)^-1, |q(z)| < 1.

Если (19) - равномерно эллиптич. уравнение

(Δ ≥ Δ₀ = const > 0), то |q(z)| ≤ q₀ = const < 1.

При изучении уравнения Бельтрами основным вопросом является построение нек-рого его гомеоморфизма для данной области S; если ω(z) - гомеоморфизм уравнения Бельтрами, реализующий топологич. отображение области S на область ω(S), то всякое другое его решение в S имеет вид

w(z) = Ф[ω(z)], (21)

где Ф - произвольная аналитич. функция в области

ω(S).

Если q(z) - измерима, q(z) ≡ 0 вне S и |q(z)| ≤ q₀ < 1, то уравнение Бельтрами (20) имеет решение вида

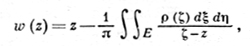
(22)

где ρ удовлетворяет сингулярному интегральному уравнению (интеграл понимается в смысле главного значения по Коши):

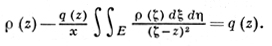
(23)

Это уравнение имеет единственное решение в нек-ром классе L_p(Е), р > 2; его можно получить методом последовательных приближений. Функция (22) принадлежит классу С_α(Е), α = р/(р - 2), реализует топологич. отображение плоскости на себя, причем w(∞) = ∞, z^-1w{z) → 1 при z → ∞. Если q ∈ C^m_α(E), 0 < α < 1, m ≥ 0, то w(z) ∈ C^m+1_α(E).

Равномерно эллиптич. система 1-го порядка общего вида в комплексной записи имеет вид

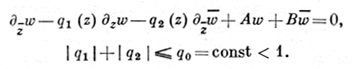
(24)

С помощью гомеоморфизма нек-рого уравнения вида (20) ее можно привести к виду (7).

Всякое решение уравнения (24) в нек-рой ограниченной области S при условии, что A, B ∈ L_p(S), р > 2, представлено в виде

w(z) = Ф[w(z)]e^φ(z) (25)

где ω(z) - некоторый гомеоморфизм уравнения Бельтрами (20) с коэффициентом

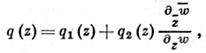
Ф(w) - аналитич. функция в области ω(S), функция φ(z) ∈ G_α(E), α = (p-2)/р голоморфна вне S и исчезает на бесконечности. Представление (25) имеет место и тогда, когда коэффициенты левой части уравнения (24) зависят от w и ее производных любого порядка, лишь бы на рассматриваемых решениях выполнялись указанные выше условия. Как и (15), формула (25) допускает обращение.

Формула (25) позволяет перенести целый ряд свойств классич. теории аналитич. функций на решения уравнения (24); теорему единственности, принцип аргумента, принцип максимума и др.

Общее квазиконформное отображение Q является решением нек-рой равномерно эллиптич. системы вида (24) (при A ≡ B ≡ 0). Справедливо и обратное утверждение. Поэтому указанные выше результаты позволяют решить чисто аналитич. путем основные проблемы квазиконформных отображений.

Системы уравнений 1-го порядка эллиптич. типа с 2n, n > 1, неизвестными функциями двух независимых переменных, при нек-рых естественных ограничениях, приводятся к канонич. виду:

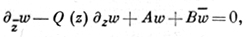
(26)

где w - искомый вектор с n комплексно значными компонентами, Q, А, В - квадратные матрицы порядка п. Теория уравнений вида (26) имеет много сходства со случаем n = 1, но она имеет и свои особенности.

Лит.: [1] Векуа И. Н., Новые методы решения эллиптических уравнений, М.- Л., 1948; [2] его же, Обобщенные аналитические функции, М., 1959; [3] его же, «Матем. сб.», 1952, т. 31, № 2, с. 217-314; [4] Бергман С., Интегральные операторы в теории линейных уравнений с частными производными, пер. с англ., М., 1964; [51 Веrs L., Theory of pseudoanalytic functions, N. Y., 1953; [6] Бояpский Б. В., «Докл. АН СССР», 1958, т. 122, № 4, с. 543-46; [7] его же, там же, 1959, т. 124, № 1, с. 15 - 18; [8] Саrlеmаn Т., «С. r. Acad. sci», 1933, t. 197, p. 471; [9] Бицадзe А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966; [10] Xалилов З. И., «Изв. АН СССР. Сер. матем.», 1947, т. 11, с. 345-62; [11] Courant R., Hilbert D., Methods of mathematical physics, v. 2, 2 ed., N. Y.-L., 1962.

И. H. Векуа.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.