ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; метод уравнений Фишера-Рисса, метод Пиконе

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; метод уравнений Фишера-Рисса, метод Пиконе,- метод решения краевых задач для Д. у. с ч. п., основанный на применении формулы Грина и приводящий к системе интегральных уравнений (Фишера - Рисса) для нек-рого подходящим образом подобранного неизвестного вектора. Метод дает возможность находить численные значения решений, но может быть применен и для доказательства теорем существования.

Пусть L* и L - сопряженные линейные эллиптические операторы 2-го порядка в пространстве точек (x₁, х₂, ..., х_n) с действительными коэффициентами

a_ik ∈ C⁽²⁾(D) ∩ C⁽¹⁾(D ∪ S), b_i ∈ C⁽¹⁾(D ∪ S), c, f ∈ C⁽⁰⁾(D ∪ S),

D - конечная область, ограниченная замкнутой поверхностью S. Пусть в классе функций, допускающих интегральные представления по формулам Грина, ищется решение u(х) задачи Дирихле:

Lu(x) = f(x), x ∈ D, lim_x→y∈S u(х) = φ(у).

Пусть, далее, v(x) - произвольная функция из того же класса. Применение формулы Грина к u(х) и v(x) приводит к соотношению

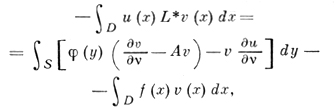
(1)

где

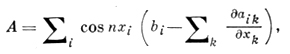
ν - внутренняя конормаль. Пусть U = (u₁, u₂) -двухкомпонентный вектор, составляющие к-рого - действительные функции с суммируемым квадратом, причем первая составляющая определена в D, а вторая -на S. Пусть L₂(D, S) - множество этих векторов; норма вводится через скалярное произведение U и V из L₂(D, S):

(U, V) = ∫_D u₁v₁ dx + ∫_S u₂v₂ dy.

Пусть {v_k} - множество, выбранное так, что совокупность двухкомпонентных векторов

V_k = (-L*v_k(x), v_k(y)), x ∈ D, y ∈ S,

полна в гильбертовом пространстве L₂(D, S). Тогда, обозначив через U = (u₁, u₂) вектор с первой составляющей u₁(х), равной u(х), и второй составляющей u₂(у), совпадающей с ∂u/∂ν, можно записать (1) в виде системы интегральных уравнений Фишера - Рисса:

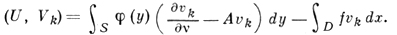
(2)

Если совокупность {V_k} ортонормирована и выполняются условия Рисса-Фишера теоремы, то система (2) определит в L₂(D, S) коэффициенты Фурье с_k вектора U = (u₁, u₂) относительно полной системы базисных векторов {V_k}. Если известно, что решение рассматриваемой задачи существует и единственно, то ряд Фурье ∑_k c_kV_k сходится в среднем к искомому решению и только к нему. В противном случае выбор функций {v_k} связан с необходимостью дополнительного исследования. Так, если допускаются собственные решения u₀(х) (нарушена единственность), совокупность должна удовлетворять равенствам

(U₀, V_k) = 0,

где U0 = (u0(x), ∂u0/∂ν). Если в качестве {vk} взята последовательность одночленов xα11xα22...xαmm с целыми неотрицательными показателями α1, α2, αm, то значения u(х) и ∂u/∂ν, найденные из (2), вместе с заданным на S значением u(х), удовлетворяют функциональным соотношениям Грина:

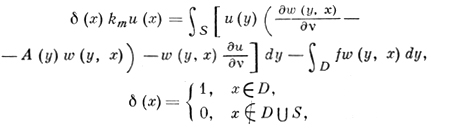
где k_m - отличная от нуля постоянная, зависящая от m, и w(y, х) - фундаментальное решение уравнения L*v = 0. В этом случае все решения системы уравнений Фишера-Рисса (2) и только они являются решениями рассматриваемой краевой задачи. Центральным пунктом этого метода является построение подходящим образом выбранной совокупности функций {v_n}, удовлетворяющих условию L*v_n = 0 либо нек-рым условиям полноты [4].

Этот способ не требует задания явного выражения фундаментального решения, но если последнее известно, то, в силу того, что совокупность {w(y, x^(k))}, где x^(k) - счетная бесконечная последовательность произвольных точек, не принадлежащих D ∪ S, линейно независима и полна в L₂(S) [4], можно значительно упростить вычисления; эта теорема позволяет также распространить метод уравнений Фишера - Рисса на задачи с косыми производными (см. Дифференциальное уравнение с частными производными; задача с косой производной) и другие типы уравнений.

Лит.: [1] Picone М., «Аtti Accad. sci. Torino. Cl. sci. lis., mat. e natur.», 1940, v. 75, p. 413-26; [2] Ameriо L., «Amer. J. Math.», 1947, v. 69, № 3, p. 447-89; [3] Fichera G., «Ann. Scuola norm. super. Pisa. Sci. fis. e mat.», 1950, t. 4, fasc. 1-2, p. 35-99; [4] Купpадзe В. Д., «Успехи матем. наук», 1967, т. 22, в. 2, с. 59-107; [5] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957.

В. Д. Нупрадзе.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.