ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача со свободными границами

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача со свободными границами - задача, в к-рой требуется найти решение системы Д. у. с ч. п. с соответствующими начальными и граничными условиями в области, граница к-рой частично или полностью неизвестна и подлежит определению. К такого типа задачам приводят многие проблемы фильтрации, диффузии, теплопроводности и др. разделов механики сплошных сред. Так, напр., задана Гельмгольца - Кирхгофа о симметричном струйном обтекании равнобочного клина с углом раствора 2απ неограниченным потоком идеальной жидкости заключается в отыскании компонент скорости u = u(х, у), v = v(x, у), являющихся решением системы уравнений Коши - Римана:

∂u/∂x + ∂v/∂y = 0, ∂u/∂y - ∂v/∂x = 0,

и удовлетворяющих на известной границе условиям (см. рис.):

v|_AO = 0, v|_OB = tg απ u|_OB.

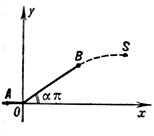
Неизвестная граница BS является линией тока, и на ней задано дополнительное условие

u² + v² = v²_∞, lim_r→∞ u = v_∞, r = √(x² + y²)

(на рис. приведена верхняя половина течения у ≥ 0, при y ≤ 0 течение симметрично).

При изучении плоских задач со свободными границами большую роль играют методы теории функций комплексного переменного.

См. также Стефана задача.

Лит.: [1] Монахов В. Н., Краевые задачи со свободными границами для эллиптических систем, Новосиб., 1977; [2] Кружков С. Н.,«Прикл. матем. и механ.», 1967, т. 31, в. 6, с.1009-20; [3] Шишкин Г. И., «Докл. АН СССР», 1971, т. 197, № 6, 1276-79.

Ф. П. Васильев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.