ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с разрывными начальными (краевыми) условиями

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с разрывными начальными (краевыми) условиями - задача для Д. у. с ч. п., в к-рой функции, задающие (начальные) краевые условия, не являются непрерывными.

Пусть, например, для гиперболического уравнения второго порядка

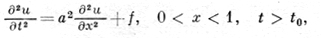
поставлена смешанная задача с начальными условиями:

∂u/∂t|_t=t0 = φ₁, u|_t=t0 = φ₀,

и краевыми условиями

u|_x=0 = ψ₁, u|_x=1 = ψ₂;

в этом смысле разрывы начальных функций φ₀ и φ₁ влекут за собой разрывы u и ∂u/∂t вдоль характеристических лучей х - at = const и x + at = const, причем мера разрыва

χ = u(с ± at + 0, t) - u(c ± at - 0, t),

или

χ = u_t(c ± at + 0, t) - ut(c ± at - 0, t),

где c ∈ [0, 1] -точка разрыва функций φ₀ или φ₁, удовлетворяет вдоль характеристического луча уравнению

dχ/dt + 0⋅λ = 0,

т. е. χ = const. Аналогичные результаты справедливы для гиперболических уравнений 2-го порядка с переменными коэффициентами:

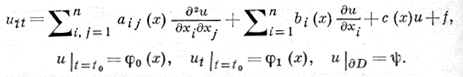
В этом случае разрывы начальных функций и краевых условий также влекут за собой разрывы u и ∂u/∂t вдоль характеристических лучей, определяемых из системы уравнений

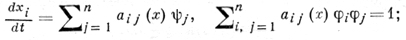
мера разрыва χ удовлетворяет уравнению:

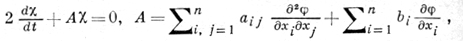
где функция φ(х) определяет характеристическую поверхность в виде уравнения φ(х) = С.

Для уравнения эллиптического типа разрывы краевых условий внутрь области D не распространяются, т. к. в этом случае характеристические лучи комплексны. Для таких уравнений эллиптического типа изучен вопрос о существовании и единственности решения и об удовлетворении решения граничным условиям. Так, для эллиптических уравнений 2-го порядка в произвольной области

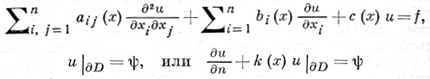
доказано, что если граничная функция ψ ∈ W^1/2₂ (∂D) для первой краевой задачи и ψ ∈ L₂(∂D) для второй краевой задачи, то существует обобщенное решение из W¹₂(D), к-рое удовлетворяет граничному условию в среднем, т. е. ||u - ψ||_L2(∂Dn) → 0, где поверхности ∂D_n аппроксимируют поверхность ∂D. В случае параболических уравнений (также как и для эллиптических уравнений) разрывы внутрь области D не распространяются, если разрывны начальные данные или краевые условия. Для этих задач изучены также вопросы о существовании и единственности обобщенного решения граничному условию.

Лит.: [1] Tихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд.,М., 1972; [2] Владимиров В. С., Уравнения математической физики, М., 1976; [3] Бицадзе А. В., Уравнения математической физики, М., 1976; [4] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [5] Берс Л., Джон Ф., Шехтер М., Уравнения с частными производными, пер. с англ., М., 1966; [6] Ладыженская О. А., Уральцева Н. Н., Линейные и квазилинейные уравнения эллиптического типа, 2 изд., М., 1973; [7] Ладыженская О. А., Солонников В. А., Уральцева Н. Н., Линейные и квазилинейные уравнения параболического типа, М., 1967; [8] Фридман А., Уравнения с частными производными параболического типа, пер. с англ., М., 1968; [9] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [10] Агмон С., Дуглис А., Ниренберг Л., Оценки решений эллиптических уравнений вблизи границы ..., пер. с англ., М., 1962.

Е. И. Моисеев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.