ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с разрывными коэффициентами

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с разрывными коэффициентами - задача для Д. у. с ч. п., в к-рой коэффициенты дифференциальных операторов испытывают разрывы 1-го рода (или скачки) при переходе через нек-рые поверхности и на этих поверхностях заданы условия сопряжения.

Задача с разрывными коэффициентами в случае эллиптич. операторов 2-го порядка (задача трансмисси и) состоит в следующем. В произвольной ограниченной открытой N-мерной области g с границей Г задана (N-1)-мерная поверхность Г₁ разбивающая область g на подобласти g₁ и g₂; в области (g + Г) ставится задача:

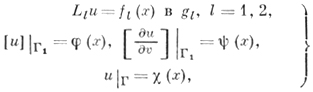
где

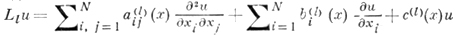
- определенный в области g_l линейный дифференциальный оператор эллиптич. типа;

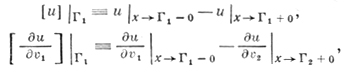
где ∂.∂v_i - производная по конормали, равная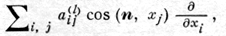

n - внешняя нормаль к Г₁, а символы Г₁ - 0 и Г₁ + 0 означают, что берутся предельные значения соответственно с внутренней и с внешней сторон поверхности Г₁ по отношению к области g₁, f_l, φ, ψ, χ - заданные функции.

Здесь для простоты считается, что имеется лишь одна поверхность разрыва коэффициентов - поверхность Г₁.

Задача (*) является математич. описанием стационарных физич. процессов, происходящих в области, составленной из различных сред, напр. рассеяния электромагнитной волны на каком-либо препятствии или распространения тепла в слоистой среде.

У задачи (*) существует классич. решение при условиях, к-рые в случае отсутствия разрыва у коэффициентов и при φ = ψ = 0 переходят в Жиро условия разрешимости задачи Дирихле (см. [3], [4], [5]). Для задачи (*) изучались: обобщенные из W^l₂ решения (см. [1], [2]); задача на собственные значения и оценки собственных функций для самосопряженных операторов L_l (см. [6], [8]); случаи вырождения в связи с марковскими процессами (см. [9], [10]); случаи с квазилинейными операторами L_l (см. [13]). Для задачи (*) могут быть установлены оценки Шаудера (см. [6], [7]); разработаны численные методы ее решения [11], [12]. Построена теория разрешимости задач с разрывными коэффициентами для эллиптич. уравнений и систем порядка 2m (см. [18], [19], [20]).

Задача с разрывными коэффициентами для параболич. и гиперболич. операторов 2-го порядка столь же подробно изучена (см. [2], [9], [14], [15], [16], [17]).

Лит.: [1] Ладыженская О. А., «Докл. АН СССР», 1954, т. 96, № 3, с. 433-36; [2] Олейник О. А., «Изв. АН СССР. Сер. матем.», 1961, т. 25, № 1, с. 3-20; [3] Ильин В. А., Шишмарев И. А., «Сиб. матем. ж.», 1961, т. 2, № 1, с. 46 - 58; [4] Ильин В. А., «Докл. АН СССР», 1961, т. 137, №. 1, с. 28-30; [5] Ладыженская О. А., Уральцева Н. И., Линейные и квазилинейные уравнения эллиптического типа, М., 1964; [6] Шишмарев И. А., «Докл. АН СССР», 1961, т. 137, № 1, с. 45-47; [7] Ван Тун, «Ж. вычисл. матем. и матем. физ.», 1964, т. 4, № 3, с. 577-80; [8] Ильин В. А., «Докл. АН СССР», 1961, т. 137, N° 2, с. 272 - 75; [9] Гирсанов И. В., «Докл. АН СССР», 1960, т. 135, № 6, с. 1311-13-[10] Фрейдлин М. И., «Докл. АН СССР», 1962, т. 144, № 3, с. 501-04; [11] Самарский А. А., в кн.: Тр. 4-го Всесоюзного матем. съезда. Ленинград, 1961, т. 2, Л., 1964; [12] его же, «Ж .вычисл. матем. и матем. физ.», 1961, т. 1, № 3, с. 441 -460; [13] Борсук М. В.,«Докл. АН СССР», 1967, т. 177, № 5, с. 991-94; [14] Камынин Л. И., в кн.: Материалы к совместному советско-американскому симпозиуму по уравнениям с частными производными, Новосиб., 1963, с. 3-6; [15] Камынин Л. И., Масленникова В. Н., «Сиб. матем. ж.», 1961, т. 2, № 3, с. 384-99; [16] Ильин В. А., «Докл. АН СССР», 1962, т. 142, № 1, с. 21-4; [17] Егоров Ю. В., «Докл. АН СССР», I960, т. 134, № 3, с. 514 - 17; [18] Schechter M., «Аnn. Scuola norm. super. Pisa. Sci. fis. e mat.», 1960, v. 14 p. 207-36; [19] Ройтберг Я. А., Шертель З. Г. «Докл. АН СССР», 1963, т. 148, № 5, с. 1034-37; [20] их же, «Успехи матем. наук», 1967, т. 22, в. 5, с. 181-82.

И. А. Шигимарев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.