ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с косой (наклонной) производной

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; задача с косой (наклонной) производной - линейная краевая задача для эллиптич. уравнений 2-го порядка.

Пусть D - область действительного евклидова пространства с декартовыми координатами х₁, х₂, ..., х_n, граница ∂D к-рой представляет собой (n-1)-мерную гиперповерхность Ляпунова. Пусть в области D задано линейное дифференциальное уравнение 2-го порядка

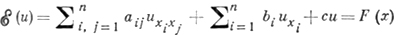
с действительными коэффициентами a_ij, b_i, с, F, удовлетворяющими условию Гёльдера в D ∪ ∂D, и, кроме того, в D соблюдено условие равномерной эллиптичности уравнения. Пусть l = (l₁, l₂, ..., l_n) - заданный на ∂D непрерывный действительный вектор, к-рый нигде не обращается в нуль. Задача с косой производной состоит в следующем: найти регулярное в области D решение u(х) уравнения (1), непрерывное в D ∪ ∂D, для к-рого в каждой точке y ∈ ∂D существует предел

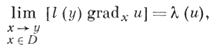
совпадающий с заданной непрерывной на ∂D функцией f(y).

λ(u) = f(y), y ∈ ∂D. (2)

В краевом условии (2) без ограничения общности можно считать, что l - единичный вектор. Неймана задача является частным случаем задачи с косой производной, когда левая часть в краевом условии (2) совпадает с производной от искомого решения по конормали ν:

du/dν = f(y), y ∈ ∂D.

Если соблюдены условия

с(х) ≤ 0 (3)

и

inf_y∈∂D(Nl) > 0, (4)

где N - внешняя нормаль ∂D в точке у, то соответствующая задаче (1), (2) однородная краевая задача

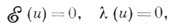
(5)

в силу принципов Хопфа и Зарембы-Жиро (см., напр., [1]), не может иметь решения, отличного от постоянной. В частности, когда в условии (3) по крайней мере в одной точке выполняется строгое неравенство, задача (1), (2) не может иметь более одного решения. При исследовании вопроса о существовании решений задачи (1), (2) обычно пользуются методом интегральных уравнений, априорными оценками или методами конечных разностей исчисления.

Выполнение условия (4) гарантирует фредгольмовость задачи (1), (2), то есть: а) размерность ϰ₁ пространства решений однородной задачи (5) конечна; б) если ϰ₁ = 0, то задача (1), (2) всегда разрешима и притом однозначно; если ϰ₁ > 0, то существует пространство линейных функционалов, обращение в нуль к-рых над F и f является условием, необходимым и достаточным для существования решений задачи (1), (2); причем размерность этого пространства также равна ϰ₁. Фредгольмовость задачи (1), (2) может нарушиться лишь тогда, когда множество М точек у, для к-рых (Nl) = 0, не пусто. В частности, при n = 2 в предположении, что

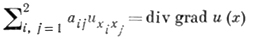
(а это не ограничивает общность), задача (1), (2) редуцируется к эквивалентному сингулярному интегральному уравнению с ядром Коши, откуда следует нётеровость задачи, то есть: а) размерность ϰ₁ пространства решений однородной задачи (5) конечна; б) размерность ϰ₂ пространства линейных функционалов, обращение в нуль к-рых над F и f является условием, необходимым и достаточным для разрешимости задачи (1), (2), также конечна; в) разность ϰ₁ - ϰ₂ = ϰ (индекс задачи (1), (2)) дается формулой ϰ = 2(p + 1),

где 2πp - приращение arg(l₁ - il₂) при однократном обходе контура ∂D области D в положительном направлении. В рассматриваемом случае задача (1), (2) будет фредгольмовой лишь при р = -1. Число р характеризует вращение векторного поля (l₁, l₂). Когда (1) представляет собой равномерно эллиптич. систему, т. е. когда F и u являются m компонентными векторами, а а_ij, b_i и с - квадратными матрицами порядка m, причем матрицы а_ij удовлетворяют условию

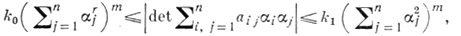
при определении оператора λ(u) в краевом условии (2) задачи с косой производной под l₁, l₂, ..., l_n следует понимать квадратные матрицы порядка m, а под f -вектор с m компонентами.

Нётеровость задачи с косой производной имеет место для широких классов равномерно эллиптич. систем и операторов λ(u). Так, напр., когда n = 2 и а_ij = 0, i ≠ j, а_ii = Е, где Е - единичная (диагональная) матрица, выполнение условия det(l₁ + il₂) ≠ 0 всюду на ∂D гарантирует нётеровость задачи (1), (2). При соблюдении этого условия индекс задачи (1), (2) вычисляется по формуле ϰ = 2(p + m), где 2πр - приращение arg det (l - il₂) при однократном обходе контура ∂D области D в положительном направлении.

С 60-х гг. 20 в. ведется интенсивное исследование задачи с косой производной при n ≥ 3 (см. [1]).

Лит.: [1] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966; [2] Векуа И. Н., Обобщенные аналитические функции, М., 1959; [3] Мусхелишвили Н. И.. Сингулярные интегральные уравнения, 3 изд., М., 1968; [4] Bouligand G., Giraud G., Delens P., Le problème de la dérivée oblique en théorle du potentiel, P., 1935.

А. В. Бицадзе.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.