ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; вариационные методы решения

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ; вариационные методы решения - методы решения краевых задач для Д. у. с ч. п. при помощи сведения этих задач (когда это возможно) к соответствующим образом подобранным вариационным задачам (т. е. к задачам на отыскание минимума или максимума нек-рого функционала) и решения последних.

Вариационные методы широко применяются как в теоретич. исследованиях (для доказательства теорем существования, единственности и устойчивости решений, при исследовании дифференциальных свойств решений, в спектральной теории, при изучении разнообразных вопросов оптимизации и т. д.), так и в вопросах, связанных с нахождением приближенных решений уравнений. Приближенные решения вариационных задач можно находить при помощи решения конечных систем алгебраич. уравнений, при этом алгоритмы нахождения приближенных решений вариационных задач часто оказываются проще и удобнее, чем имеющиеся алгоритмы решения соответствующих задач для Д. у. с ч. п.

Вариационный метод исследования краевых задач возник в сер. 19 в. в виде так наз. Дирихле принципа отыскания в области G гармония, функции, принимающей на границе ∂G области G данное значение φ(х), x ∈ ∂G, как функции, дающей в рассматриваемом классе функций минимум интегралу Дирихле. Первоначально принцип Дирихле применялся лишь в теории линейных эллиптич. уравнений 2-го порядка (впоследствии и более высоких порядков), а затем и в теории уравнений других типов, причем не только линейных, но и нелинейных. Разработке вариационных методов были посвящены работы Б. Римана (В. Riemann), К. Вейерштрасса (К. Weierstrass), Д. Гильберта (D. Hilbert). Большую роль в развитии вариационных методов, в частности в вопросе их обоснования, сыграли вложения теоремы и их обобщения.

Одним из простых и типичных примеров использования вариационных методов является решение Дирихле задачи для эллиптического самосопряженного уравнения 2-го порядка

Аu + сu = 0, (1)

где с = с(х) ≥ 0,

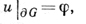
(2)

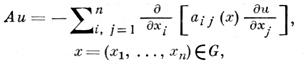
(3)

(G - область конечномерного евклидова пространства, ∂G - ее граница, φ - заданная на ∂G функция), и существует постоянная ϰ > 0 такая, что для всех точек x ∈ G и всех чисел ξ₁ ξ₂, ..., ξ_n выполняется неравенство (условие эллиптичности)

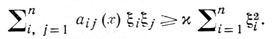
В этом случае вариационный метод решения задачи (1) - (2) состоит в отыскании функции u(х), для к-рой функционал

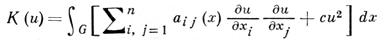
(уравнение (1) является Эйлера уравнением для функционала К(u)) принимает наименьшее значение в классе допустимых функций, т. е. таких функций u(х), для к-рых A(u) < +∞, и выполняется граничное условие (2). Вариационный метод применим только тогда, когда класс допустимых функций не пуст. Условия, к-рым должна удовлетворять заданная на границе функция φ для того, чтобы класс допустимых функций был не пуст, даются теоремами вложения. Функция u(х), для к-рой функционал К(u) принимает наименьшее значение в классе допустимых функций, является обобщенным решением задачи (1)-(2) (см. Дифференциальное уравнение с частными производными; функциональные методы решения) и, напр., в классическом случае непрерывной дифференцируемости коэффициентов a_ij(x) оператора (3) - обычным решением этой задачи.

Другим типичным примером использования вариационных методов является их применение к отысканию собственных значений и собственных функций оператора (3).

Функция, дающая минимум нек-рому функционалу, может быть получена как предел так наз. минимизирующей последовательности, т. е. последовательности функций, значения функционала на членах к-рой стремятся к указанному минимуму. Для построения минимизирующих последовательностей и установления скорости их сходимости разработаны специальные методы (напр., Ритца метод).

Лит.: [1] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [2] его же, Принцип Дирихле, конформные отображения и минимальные поверхности, пер. с англ., М., 1953; [3] Соболев С. Л., Некоторые применения функционального анализа в математической физике, Новосиб., 1962; [4] Смирнов В. И., Курс высшей математики, т. 3-5, М., 1958-59; [5] Михлин С. Г., Вариационные методы в математической физике, 2 изд., М., 1970; [6] Ладыженская О. А., Уральцева Н. Н., Линейные и квазилинейные уравнения эллиптического типа, 2 изд., М., 1973; [7] Михайлов В. П., Дифференциальные уравнения в частных производных, М., 1976.

Л. Д. Кудрявцев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.