
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ОТКЛОНЯЮЩИМСЯ АРГУМЕНТОМ
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ОТКЛОНЯЮЩИМСЯ АРГУМЕНТОМ - дифференциальное уравнение, связывающее аргумент, искомую функцию и ее производные, взятые, вообще говоря, при различных значениях этого аргумента. Примеры:
х'(t) = ax(t - τ), (1)
х'(t) = ax(kt), (2)
где постоянные а, τ, k заданы; τ в уравнении (1) и t - kt в уравнении (2) - отклонения аргумента. Встречаются и более сложные Д. у. с о. а., включающие большее число отклонений аргумента, могущих представлять собой заданные функции (в частности, если они постоянны, то уравнение часто наз. дифференциально-разностным) или даже зависеть от искомого решения. Эпизодически рассматривались также Д. у. с о. а., в к-рых искомая функция зависит более чем от одного аргумента. Д. у. с о. а. впервые появились в связи с формальным решением уравнений с частными производными и затем неоднократно рассматривались как сами по себе, так и в связи с задачами геометрии, а позднее - в связи с различными приложениями, прежде всего к теории автоматич. управления. Построение систематич. теории Д. у. с о. а. было начато в 1949.
Определение Д. у. с о. а. допускает любые суперпозиции искомого решения [типа x(x(t))] и интегралы от него, поэтому формально класс Д. у. с о. а. включает в себя все уравнения математич. анализа. Все же обычно, говоря о Д. у. с о. а., имеют в виду тот или иной естественный класс дифференциальных уравнений, в к-рых введено отклонение аргумента, допускающее построение содержательной теории. При этом ряд свойств Д. у. с о. а. имеет непосредственную аналогию со свойствами обычных дифференциальных уравнений, тогда как иные свойства являются принципиально новыми.
Уравнение (или система уравнений)
x(n)(t) = f(t; x(m1)(t - τ1), ..., x(m1)(t - τs)) (3)
(для системы х и f - векторы), где все τj ≥ 0, наз. уравнением (системой) запаздывающего, нейтрального или опережающего типа, если maxjmj < n, = n, > n, соответственно. Для уравнений иных видов такая классификация проводится на основе преобразования к виду (3)
помощью замены t → χ(t), χ - возрастающая функция; напр., уравнение (1) запаздывающего типа при τ ≥ 0 и опережающего (замена t → t + τ) - при τ < 0. Если отклонения τj зависят от t, то уравнение (3) может менять тип; напр., уравнение (2) для k ≤ 1 запаздывающего типа при t ≥ 0 и опережающего - при t ≤ 0. Если τj зависят от искомого решения, то уравнение (3) может иметь различный тип для различных его решений. Наиболее подробно разработана теория Д. у. с о. а. запаздывающего типа, менее - нейтрального типа и почти не изучена теория уравнений опережающего типа.
Один из простейших классов Д. у. с о. а. следующий:
x'(t) = f(t, x(t), x(t - τ)), τ > 0. (4)
Для этого класса Д. у. с о. а. ставится основная начальная задача: заданы начальная точка t0, начальная функция φ(t), t0 - τ ≤ t ≤ t0, и значение x(t0 + 0); под решением задачи для уравнения (4) понимается функция x{t), t > t0, обращающая уравнение (4) в тождество, причем при t > t0, t - τ ≤ t0 в правую часть вместо x(t - τ) надо подставлять φ(t - τ). Для решения поставленной задачи можно применить метод шагов: при t0 < t ≤ t0 + τ решают начальную задачу для уравнения (4), в к-ром вместо x(t - τ) подставлено φ(t - τ); при t0 + τ < t ≤ t0 + 2τ будет t0 < t - τ ≤ t0 + τ, т. е. x(t - τ) уже построено, и т. д.; таким образом, на каждом шаге приходится решать задачу Коши для уравнения без отклонения аргумента. Если функции f и φ непрерывны и x(t0 + 0) = φ(t0), то решение задачи существует на нек-ром интервале t0 < t ≤ t0 + h и может быть продолжено обычным образом, а если функция f(t, х, у) удовлетворяет по х условию Липшица, то это решение единственно и непрерывно зависит от f, φ, τ. Если при этом функция f достаточно гладкая, то х'(t) непрерывна при t > t0, х''(t) непрерывна при t > t0 + τ и т. д. (свойство сглаживания).
Аналогично ставится начальная задача и строится решение для систем уравнений вида (4) и для уравнений высших порядков. В случае нескольких запаздываний за шаг принимают наименьшее из них. Если τ = τ(t), то φ(t) должна быть задана на всем начальном множестве значений t - τ(t) ≤ t0, t > t0. Наличие у τ(t) нулей препятствует применению метода шагов, однако с помощью простых аппроксимационных
или итерационных методов можно доказать теорему о разрешимости начальной задачи, аналогичную приведенной выше. Численные методы ее решения в принципе те же, что для τ ≡ 0. Если заданные функции разрывны или x(t0 + 0) ≠ φ(t0), то понятие решения должно быть естественно обобщено.
Решение сформулированной начальной задачи строится только в направлении возрастания t. Другая ее особенность состоит в том, что многообразие решений при произвольной φ(t), вообще говоря, бесконечномерное. (Исключением служат уравнения без предыстории, для к-рых t0 ≤ t - τ(t) ≤ t при t ≥ t0;
напр., уравнение (2) при 0 ≤ k ≤ 1, t0 = 0.) Это существенно отличает теорию Д. у. с о. а. от теории уравнений без отклонения аргумента.
В уравнении (4) запаздывание сосредоточенное. Рассматриваются также уравнения с распределенным запаздыванием, правая часть к-рых включает интегралы
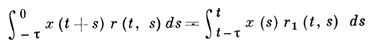
(это - интегро-дифференциальные уравнения типа Вольтерра) или, комбинированный случай,
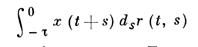
и т. п. Наиболее общим видом Д. у. с о. а. запаздывающего типа 1-го порядка служит дифференциально-функциональное уравнение типа Вольтерра
х'(t) = F[x(t + s); t], -τ ≤ s ≤ 0,
где правая часть при каждом t > t0 представляет собой функционал. И для таких уравнений начальная задача разрешима.
Для Д. у. с о. а. нейтрального типа, напр. x'(t) = f(t, x(t), x(t - τ1), х'(t - τ2)), τ1, τ2 ≥ 0,
постановка и свойства начальной задачи аналогичны указанным выше, однако свойство сглаживания отсутствует; кроме того, возможны осложнения, если переменное запаздывание τ2(t) имеет нули. Начальная задача для Д. у. с о. а. опережающего типа является некорректной.
Лучше других изучены линейные автономные (т. е. с постоянными коэффициентами и постоянными отклонениями аргумента) Д. у. с о. а. Уравнение (без подобных членов)
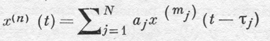
(5)
(все aj ≠ 0) имеет частные решения х = еpt, где р удовлетворяет характеристическому уравнению
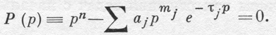
(6)
Здесь Р(р) - квазиполином; k-кратному корню уравнения (6) отвечают решения ept, ..., tk-1ept уравнения (5). Если хотя бы одно τj ≠ 0, то уравнение (6) имеет бесконечное число корней р1, р2, ... Чтобы уравнение (5) имело запаздывающий (нейтральный) тип, необходимо и достаточно условие
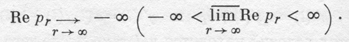
В этих случаях каждое решение уравнения (5) разлагается в ряд по указанным частным решениям, а при решении начальной задачи для уравнения (5) и соответствующего неоднородного уравнения можно пользоваться обычными методами операционного исчисления. Аналогичными свойствами обладают системы уравнений и уравнения с распределенным запаздыванием.
с коэффициентами Aij, зависящими только от точки x ∈ D. В каждой точке x ∈ D квадратичная форма Q при помощи неособого аффинного преобразования переменных λc = ζ0(ξ1, ..., ξn) i = 1, ..., n, может быть приведена к канонич. виду
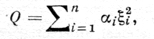
где коэффициенты αi, i = 1, ..., n, принимают значения 1, -1, 0, причем число отрицательных коэффициентов (индекс инерции) и число нулевых коэффициентов (дефект формы) являются аффинными инвариантами. Когда все αi = 1 или все αi = -1, т. е. когда форма Q соответственно положительно или отрицательно определена (дефинитна), уравнение (3) наз. эллиптическим в точке x ∈ D. Если один из коэффициентов αi отрицателен, а все остальные положительны (или наоборот), то уравнение (3) наз. гиперболическим в точке х. В случае, когда l, 1 < l < n-1, коэффициентов αi положительны, а остальные n-l отрицательны, уравнение (3) наз. ультрагиперболическим. Если же хотя бы один из этих коэффициентов (но не все) равен нулю, то уравнение (3) наз. параболическим в точке х. Говорят, что в области D своего задания уравнение (3) является уравнением эллиптического, гиперболического или параболического типа, если оно соответственно эллиптично, гиперболично или параболично в каждой точке этой области. Эллиптическое в области D уравнение (3) наз. равномерно эллиптическим, если существуют действительные числа k0 и k1 одинакового знака такие, что
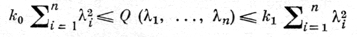
для всех x ∈ D. Когда в разных частях области D уравнение (3) принадлежит к различным типам, то говорят, что оно является уравнением смешанного типа в этой области. Лапласа уравнение
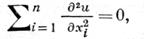
теплопроводности уравнение
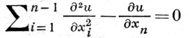
и волновое уравнение
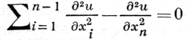
являются типичными примерами линейных эллиптич., параболич. и гиперболич. уравнений 2-го порядка соответственно (подробнее см. Линейное гиперболическое уравнение и система, Линейное параболическое уравнение и система, Линейное эллиптическое уравнение и система).
Трикоми уравнение
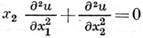
относится к уравнениям смешанного типа в любой области плоскости переменных х1, х2, пересечение к-рой с осью х2 = 0 не пусто (подробнее см. Смешанного типа уравнение с частными производными).
В случае линейного уравнения с частными производными порядка m
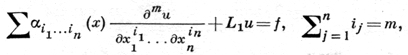
где L1 - линейный дифференциальный оператор с частными производными порядка ниже т, форма (2) имеет вид
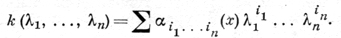
(5)
Если при фиксированном значении x ∈ D можно найти такое аффинное преобразование λi = λi(μ1, ..., μn), i = 1, ..., n, в результате к-рого полученная из (5) форма содержит лишь l, 0 < l < n, переменных μ, то говорят, что уравнение (4) в точке х параболически вырождается. При отсутствии параболич. вырождения и если конич. многообразие
k(λ1, ..., λn) = 0 (6)
не имеет действительных точек, кроме λ1 = 0, ..., λn = 0, то уравнение (4) в точке х наз. эллиптическим. Уравнение (4) наз. гиперболическим в точке х, если в пространстве переменных λ1, ..., λn существует прямая δ такая, что если принять ее за координатную прямую в новых переменных μ1, ..., μn, полученных аффинным преобразованием λ1, ..., λn, то относительно координаты, изменяющейся вдоль δ, преобразованное уравнение (6) имеет ровно m действительных корней (простых или кратных) при любом выборе остальных координат μ.
Аналогичным образом по характеру формы (2) происходит классификация по типам уравнения (1) и в нелинейном случае. Поскольку в этом случае коэффициенты формы (2) зависят, наряду с точкой х, от искомого решения и от его производных, классификация по типам имеет смысл лишь для этого решения. См. также Нелинейное уравнение с частными производными.
Когда F представляет собой N-мерный вектор F = (F1, ..., FN) с компонентами
Fi(x, ..., pi1...in, ...), i = 1, 2, ..., N,
зависящими от x ∈ D и от М-мерных векторов 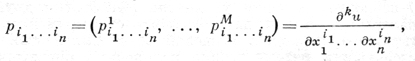
векторное равенство (1) наз. системой дифференциальных уравнений с частными производными относительно неизвестных функций u1, ..., uM или относительно неизвестного вектора u = (u1, ..., uM). Максимальный порядок производных от искомых функций, входящих в данное уравнение системы, наз. порядком этой системы (уравнения). Когда M = N и порядок каждого уравнения системы (1) равен m, определитель
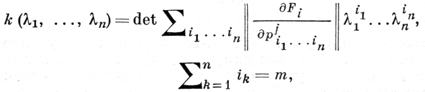
(7)
где
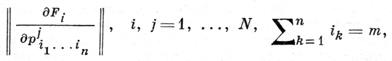
- квадратная матрица, представляет собой форму порядка Nm относительно действительных скалярных параметров λ1, ..., λn и наз. характеристическим детерминантом системы (1). Классификация по типам системы (1) происходит по характеру формы (7) точно так же, как при рассмотрении одного уравнения порядка m. Фигурирующие в левой части уравнения (1) величины могут быть комплексными. Комплексное Д. у. с ч. п. очевидным образом заменяется системой Д. у. с ч. п.
Д. у. с ч. п. может вовсе не иметь решения. Однако встречающиеся в приложениях Д. у. с ч. п., как правило, имеют целые семейства решений. При выводе этих уравнений из общих законов, к-рым подчинены изучаемые явления природы, естественно возникают дополнительные условия, налагаемые на искомые решения. Центральное место в теории Д. у. с ч. п. занимают задачи отыскания именно таких регулярных решений, к-рые удовлетворяют этим условиям. Условия задач, к-рым должно удовлетворять искомое решение, существенно зависят от типа рассматриваемого уравнения.
Для эллиптич. уравнений обычно рассматриваются так наз. краевые задачи, к-рые, напр., в случае уравнения 2-го порядка в основном охватываются следующей постановкой: ищется регулярное в области D решение и(х) уравнения (1), удовлетворяющее условию
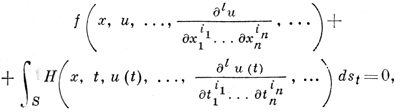
(8)
где S - граница области D, f и Н - заданные действительные функции, dst - элемент площади поверхности S, а под
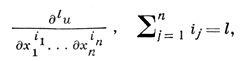
при х ∈ S понимаются пределы соответствующих производных функции u(х), когда точка х изнутри области D стремится к S.
В такой общей постановке задача (8) далека от своего сколько-нибудь полного решения. Сравнительно хорошо исследованы такие частные случаи этой задачи, какими являются так наз. первая и вторая краевые задачи (см. Дирихле задача и Неймана задача) для линейных уравнений, удовлетворяющих условию равномерной эллиптичности.
В отличие от краевых задач для эллиптич. уравнений, в к-рых носителем данных является вся граница области, где ищется решение, для широких классов уравнений гиперболич. и параболич. типов носителями дополнительных данных могут служить определенным образом ориентированные незамкнутые поверхности пространства Еn, причем от них существенно зависит область определения искомого решения. К таким задачам относятся, напр., Коши задача с начальными данными, характеристическая задача Коши. Особо ставятся краевые задачи для уравнений смешанного типа. В теории Д. у. с ч. п. значительное внимание уделяется обширному классу смешанных задач. См. Смешанная задача для гиперболического уравнения и системы, Смешанная и краевая задачи для параболического уравнения и системы.
Задача считается в классич. смысле корректно (правильно) поставленной, если она имеет и притом единственное устойчивое решение. Задачи, не удовлетворяющие этим требованиям, до недавнего времени считались лишенными смысла. Начиная с 40-х гг. 20 в. широта диапазона математич. проблем физики, механики и техники заставила расширить не только понятие корректности постановок задач для Д. у. с ч. п., но и понятие самого решения. Были введены так наз. обобщенные решения. Наряду с вопросами существования и единственности точных решений тех или иных задач для Д. у. с ч. п. в приложениях значительную важность приобрели понятия в определенном смысле приближенных решений и фактическое построение таких решений.
Исторически одним из первых методов, позволяющих строить решения ряда задач для важных классов Д. у. с ч. п., является метод разделения переменных, или Фурье метод, к к-рому тесно примыкает метод интегральных преобразований (см. Фурье интеграл). От применения этого метода берет свое начало спектральная теория дифференциальных операторов.
Сравнительно позже был создан параметрикса метод, на основе к-рого построен потенциалов метод. Этот метод позволяет привлекать к исследованию краевых задач для эллиптич. уравнений аппарат интегральных уравнений. Далеко идущим развитием метода параметрикса являются методы теории функций комплексного переменного, успешно применяющиеся при исследовании эллиптич. уравнений с двумя независимыми переменными. См. Дифференциальное уравнение с частными производными; методы комплексного переменного.
Когда изучаемое Д. у. с ч. п. представляет собой уравнение Эйлера для многомерной задачи вариационного исчисления, часто пользуются вариационным методом. Вариационный метод весьма удобен в тех случаях, когда уравнение Эйлера является уравнением эллиптич. типа. См. также Дифференциальное уравнение с частными производными; вариационные методы решения.
Начиная с 30-х гг. 20 в. при исследовании Д. у. с ч. п. широко используются методы функционального анализа, среди к-рых центральное место занимают Шаудера метод и его дальнейшее развитие - метод априорных оценок. Эти методы позволяют сравнительно легко установить существование слабых решений и сильных решений как для линейных, так и для нек-рых классов нелинейных Д. у. с ч. п. См. Дифференциальное уравнение с частными производными; функциональные методы решения.
Среди методов, успешно приводящих к цели при построении приближенных решений Д. у. с ч. п., чаще всего применяются методы конечных разностей исчисления. См. также Гиперболического типа уравнение, численные методы решения; Параболического типа уравнение, численные методы решения; Эллиптического типа уравнение, численные методы решения.
Лит.: [1] Берс Л., Джон Ф., Шехтер М., Уравнения с частными производными, пер. с англ., М., 1966; [2] Бицадзе А. В., Уравнения математической физики, М., 1976; [3] Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; [4] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [5] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972.
А. В. Бицадзе.
Источники:
- Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'