ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ АБСТРАКТНОЕ

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ АБСТРАКТНОЕ - дифференциальное уравнение в том или ином абстрактном пространстве (гильбертовом, банаховом и т. п.) или дифференциальное уравнение с операторными коэффициентами. Классическим и наиболее часто встречающимся Д. у. а. является уравнение

Lu ≡ ∂u/∂t - Au = f, (1)

где неизвестная функция u = u(t) принадлежит нек-рому функциональному пространству X, 0 ≤ t ≤ T ≤ ∞, и А: Х → Х - оператор (как правило - линейный), действующий в этом пространстве. Если оператор А ограничен и постоянен (не зависит от t), то формула

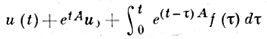
дает единственное решение уравнения (1), удовлетворяющее условию u(0) = u₀. Для переменного A (t) оператор e^(t-τ)A заменяется эволюционным оператором u(t, τ). В случае неограниченного оператора А решения задачи Коши u(0) = u₀ могут: не существовать при нек-рых u₀, быть не единственными, обрываться при t < T. Исчерпывающее изучение однородного (f ≡ 0) уравнения (1) с постоянным оператором дается теорией полугрупп, а вопросы существования и единственности решаются в терминах свойств резольвенты А (см. [1], [5]). Этот же метод применим и для переменного оператора при условиях его гладкой зависимости от t (см. [5]). Другим методом изучения уравнения (1), дающим, как правило, более грубые результаты, но применимым к более широким классам уравнений (в некоторых случаях - даже к нелинейным), является использование энергетич. неравенств: ||u|| ≤ c||Lu||, получаемых также за счет тех или иных предположений относительно А. Для гильбертова пространства X постулируются, как правило, различные свойства положительности скалярного произведения (Аu, u) (см. [2]). Все сказанное в значительной степени распространяется и на более общее Д. у. а.

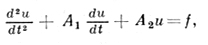
(2)

рассматриваемое при условиях u(0) = u₀, u'_t(0) = u₁. Зачастую, изучение уравнения (2) тем или иным приемом (сведением к системе уравнений 1-го порядка,

заменой 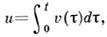, расщеплением левой части на

произведение двух операторов 1-го порядка и т. п.) сводится к изучению уравнения (1). Основным источником интереса к Д. у. а. является возможность сведения к уравнениям вида (1) или (2) так наз. смешанных задач в цилиндрич. областях для классических параболич. и гиперболич. уравнений 2-го порядка: функция u(t, х₁, ..., х_n) рассматривается как функция t со значениями в соответствующем пространстве функций от х, а дифференцирования по х, вместе с граничными условиями на боковых поверхностях цилиндра (образующие к-рого параллельны оси t), порождают операторы A, A_k. Уравнения (1), (2), в к-рых постулируемые свойства операторов A, A_k совпадают с получающимися в описанной выше ситуации, наз. абстрактными параболическими или гиперболическими. Реже рассматриваются абстрактные эллиптич. операторы.

Часто формулируются в терминах полугрупп и уравнения (1) задачи в теории рассеяния [3], рассматривающей интервал -∞ < t < +∞. Сведение задач для дифференциальных уравнений с частными производными к задачам для Д. у. а. (1) и (2) оказывается весьма удобным при разработке приближенных (напр., разностных [4]) методов решения и при рассмотрении асимптотич. методов («малый» и «большой» параметры). Общие Д. у. а. с оператором

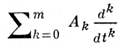
и граничными условиями на обоих концах интервала (0, Т) при неограниченных операторах А_k поддаются содержательному изучению лишь при весьма специальных предположениях относительно А_k. Для ограниченных А_k соответствующее обобщение теории обыкновенных дифференциальных уравнений не вызывает затруднений.

Лит.: [1] Xилле Э., Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., [2 изд.], М., 1962; [2] Liоns J., Equations differentielles operatiounelles et problemes aux limites, В., 1961; [3] Лакс П., Филлипс Р., Теория рассеяния, пер. с англ., М., 1971; [4] Самарский А. А., Введение в теорию разностных схем, М., 1971; [5] Крейн С. Г., Линейные уравнения в банаховом пространстве, М., 1971.

А. А. Цезии.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.