
ДИФФЕРЕНЦИАЛЬНОЕ НЕРАВЕНСТВО
ДИФФЕРЕНЦИАЛЬНОЕ НЕРАВЕНСТВО - неравенство, связывающее аргумент, неизвестную функцию и ее производные, напр.,
y'(x) > f(x, у(х)), (1)
где у(х) - неизвестная функция аргумента х. Основная проблема теории Д. н. - по заданному Д. н. и дополнительным (начальным или граничным) условиям описать совокупность всех его решений.
Большую группу составляют Д. н., получающиеся из дифференциальных уравнений хорошо изученных классов заменой знака равенства на знак неравенства, что равносильно добавлению к одной из частей уравнения заранее не уточняемой функции определенного знака. Представляет интерес сравнение решений таких Д. н. с решениями соответствующих дифференциальных уравнений. Так, для любого решения Д. н. (1) справедливы оценки [1]:
у(х) < z(х) при x1 ≤ х < х0,
у(х) > z(х) при х0 < x ≤ x2,
где
z' = f(х, z), z(х0) = у(х0),
на любом интервале [х1, х2] существования обоих решений. Это простое утверждение широко применяется для оценок решений дифференциальных уравнений (путем перехода к соответствующему Д. п. с легко указываемым частным решением), области продолжимости решений, разности между двумя решениями, для вывода условий единственности решения и т. д. Справедливо аналогичное утверждение [2] и для Д. н. (неравенство Чаплыгина)
y(m) + a1(х)y(m-1) + ... + am(x)y > f(x).
Здесь оценки типа (2) для решений, удовлетворяющих при х = х0 одинаковым начальным условиям, гарантируются лишь на интервале, определяемом коэффициентами a1, ..., аm: напр., для Д. н. y'' + y > f(x) это интервал [х0 - π, x0 + π].
Для системы Д. н.
y'i(x) > fi(х, y1, ..., yn) (i = 1, ..., n)
было указано [3], что если каждая функция fi не убывает по аргументам yj(∃j≠i), то имеет место оценка
yi(х) > zi(х) при х0 < х ≤ х2; i = 1, ..., n,
подобная (2). Развитие этих рассмотрений приводит к теории Д. н. в пространствах с конусом.
Разновидностью Д. н. является требование знакопостоянства полной производной от заданной функции:
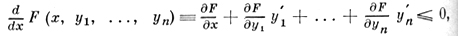
применяемое в теории устойчивости.
Представителем другой группы является Д. и.
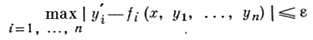
(ε > 0 задано), исследованное впервые в связи с общей концепцией о приближенном описании реальной задачи дифференциальными уравнениями [4]. Здесь интересно описание интегральной воронки, т. е. совокупности всех точек всех решений, удовлетворяющих заданным начальным условиям, в частности поведение воронки при х → ∞. Естественным обобщением Д. н. (3) является дифференциальное уравнение в контингенциях, к-рое задается с помощью поля конусов, обобщающего понятие поля направлений.
Для Д. н. изучалась и теория краевых задач. Д. н. Δu ≥ 0 (Δ - оператор Лапласа) определяет субгармонические функции, Д.н. ∂u/∂t -Δu ≤ 0
определяет субпараболические функции. Рассматривались и более общего вида Д. н. (обеих упомянутых выше групп) с частными производными для дифференциальных операторов различных типов.
Лит.: [1] Petrovitsch М., «Math. Ann.», 1901, Bd 54, № 3, S. 417-36; [2] Чаплыгин С. А., Основания нового способа приближенного интегрирования дифференциальных уравнений, М., 1919; [3] Wazewski Т., «Аnn. Soc. polon. math.», 1950, t. 23, p. 112-66; [4] Вohl P., «J. reine und angew. Math.», 1914, Bd 144, S. 284-313; [5] Нааr А., в кн.: «Atti del Congresso Internazionale dei Mathematici. Bologna». 1928, t. 3, Bologna, 1930, p. 5-10; [6] Walter W., Differentialund Integral-Ungleichungen und ihre Anwendung bei Abschät-zungs- und Eindeutigkeitsproblemen, В., 1964; [7] Szarski J., Differential inequalities, Wars., 1965; [8] Lakshmikantham V., Leela S., Differential and integral inequalities, v. 1-2, N. Y., 1969.
А. Д. Мышкис.
Источники:
- Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'