ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ на аналитических пространствах - обобщение классич. исчисления дифференциальных форм и дифференциальных операторов на случай аналитич. пространств. Об исчислении дифференциальных форм на комплексных многообразиях см. Дифференциальная форма. Пусть (X, 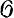_X) - аналитич. пространство над полем k, Δ - диагональ в X × X, J - пучок идеалов, определяющий Δ и порожденный всеми ростками вида π*₁f - π*₂f, где f - произвольный росток из 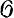_X, π_i: Х × Х → X - проекция на i-й сомножитель.

Аналитич. пучок π₁(J/J²) = Ω_X наз. пучком аналитических дифференциальных форм первой степени на X. Если f - росток аналитич. функции на X, то росток π*₁f - π*₂f принадлежит J и определяет элемент df пучка Ω¹_X, π₁J/J²), называемый дифференциалом ростка f. Тем самым определяется гомоморфизм пучков векторных

пространств d: 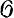_X → Ω¹_X. Если Х = kⁿ, то Ω¹_X - свободный пучок, порожденный dx₁, ..., dx_n, где x₁, ..., х_n -координаты в kⁿ. Если X - аналитич. подпространство в kⁿ, определяемое пучком идеалов J, то

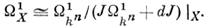
С каждым аналитич. отображением f : X → Y можно связать пучок относительных дифференциалов Ω¹_X. Это - аналитич. пучок Ω¹_X/Y, индуцирующий Ω¹_Xs на каждом слое X_s(s ∈ Y) отображения f; он определяется из точной последовательности

f*Ω¹_Y → Ω¹_X → Ω¹_X/Y → 0.

Пучок Θ_X = Ноm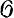_X (Ω¹_X, 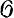_X) наз. пучком ростков аналитических векторных полей на X. Если X - многообразие, то Ω¹_X и 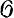_X -локально свободные пучки, естественно изоморфные пучкам ростков аналитич. сечений кокасательного и касательного расслоений над X соответственно.

Аналитич. пучки 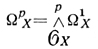наз. пучками аналитических внешних дифференциальных форм степени р на X (при k = ℂ их наз. также голоморфными формами). Для всякого р ≥ 0 определяется гомоморфизм пучков векторных пространств d^p: Ω^p_X → Ω^p+1_X, совпадающий при р = 0 с введенным выше и удовлетворяющий условию d^p+1d^p = 0. Комплекс пучков (Ω*_X, d) наз. комплексом де Рама пространства X. Если X - многообразие и k = ℂ или ℝ, то комплекс де Рама является точным комплексом пучков. Если X многообразие Штейна или вещественное аналитич. многообразие, то когомологии комплекса сечений Г(Ω*_X), часто также называемого комплексом де Рама, изоморфны Н^з(Х, k).

Если X имеет особые точки, то комплекс де Рама не обязан быть точным. В случае, когда k = ℂ, достаточным условием точности комплекса де Рама в точке х ∈ Х является наличие у х комплексно аналитически стягиваемой окрестности. Гипергомологии комплекса Г(Ω*_X) при k = ℂ содержат когомологии пространства X с коэффициентами в ℂ в качестве прямого слагаемого и совпадают с ними, если X гладко. Сечения пучка Θ_X наз. аналитическими (а при k = ℂ также голоморфными) векторными полями на X. Поле Z ∈ Г(X, Θ_X) определяет для любого открытого U ⊂ X дифференцирование алгебры аналитич. функций Г(U, 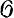_X), действующее по формуле φ → Zφ = Z(dφ). Если k = ℂ или ℝ, то Z задает локальную однопараметрич. группу expt Z автоморфизмов пространства X. Если при этом X компактно, то группа expt Z определима глобально.

Пространство Г(X, Θ_X), снабженное скобкой Ли, является алгеброй Ли над k. Если X - компактное комплексное пространство, то Г(X, Θ_X) - алгебра Ли группы Aut X.

Дифференциальные операторы на аналитич. пространстве (X, ,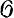_X) определяются аналогично дифференциальным операторам модуля. Если F, G - аналитич. пучки на X, то линейным дифференциальным оператором порядка действующим из F в G, наз. гомоморфизм пучков векторных пространств F → G, продолжающийся до аналитич. гомоморфизма F ⊗ π₁ (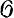_X×X/I^l+1) → G. Если X гладко, a F и G локально свободны, то это определение приводит к обычному понятию дифференциального оператора на векторном расслоении [3], [4].

Ростки линейных дифференциальных операторов F → G образуют аналитич. пучок Diff(F, G) с фильтрацией

Diff⁰(F, G) ⊂ Diff¹(F, G) ⊂ ... ⊂ Diff^l(F, G) ⊂ ...,

где Diff^l(F, G) - пучок ростков операторов порядка < l. В частности, Diff (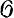, 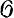) - фильтрованный пучок ассоциативных алгебр над k относительно композиции отображений. Имеем

Diff⁰(F, G) ≅ Hom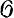(F, G),

Diff¹(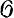, 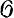)/Diff⁰(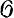, 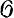) ≅ Θ_X.

Изучение пучка Diff(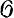, 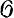) проведено (в негладком случае) лишь для нек-рых специальных типов особых точек. В частности, в случае неприводимого одномерного комплексного пространства X доказано, что пучок алгебр Diff(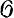, 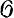) и соответствующий пучок градуированных алгебр допускают конечные системы образующих [5].

Лит.: [1] Malgrange В., «Enseign. math.», 1968, ser. 2, t. 14, № 1, p. 1-20- [2] Коup W., «Math. Ann.», 1965, Bd 160, № 1, S. 72-92; [3] Шварц Л., Комплексные многообразия. Эллиптические уравнения с частными производными, пер. с нем., М., 1964; [4] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976; [5] Вlооm Тh., «Ricе Univ. Stud.», 1973, v. 59, № 2, p. 13-19; [6] Вerger R., [u. a.], Differentialrechnung in der anaytilschen Geometrie, В.-Hdlb.-N. Y., 1967; [7] Fisсher G., Complex analytic geometry, B.-Hdlb.-N. Y., 1976.

Д. А. Пономарев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.