ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ - раздел математики, в к-ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу математич. анализа, имеющего чрезвычайное значение для естествознания и техники. Основной предпосылкой для создания Д. и. явилось введение в математику переменных величин (Р. Декарт, R. Descartes). В общих чертах построение дифференциального и интегрального исчислений было завершено в трудах И. Ньютона (I. Newton) и Г. Лейбница (G. Leibniz) к концу 17 в., однако вопросы обоснования с помощью понятия пре-

дела были разработаны О. Коши (A. Couchy) лишь в начале 19 в. Создание дифференциального и интегрального исчисления явилось началом периода бурного развития математики и связанных с ней прикладных наук. Под Д. и. обычно понимают классич. Д. и., в к-ром рассматриваются действительные функции одного или нескольких действительных переменных, хотя в современном толковании может идти речь и о Д. и. в абстрактных пространствах. Д. и. основано на понятиях действительного числа, функции, предела и непрерывности - важнейших понятий математики, сформировавшихся и получивших современное содержание в процессе развития математич. анализа и работы над его обоснованием. Центральные понятия Д. и.- производная и дифференциал - и разработанный в Д. и. аппарат, связанный с ними, доставляют средства для исследований функций, локально сходных с линейной функцией или многочленом, а именно такие функции в первую очередь интересны для приложений.

Производная. Пусть функция y = f(x) определена в нек-рой окрестности точки х₀, Δ ≠ 0 есть приращение аргумента, Δy = f(x₀ + Δx) - f(x₀) - соответствующее приращение функции. Если существует (конечный или бесконечный) предел lim_Δx→0 Δy/Δx,

то он наз. производной функции f(x) в точке х₀ и обозначается f(х₀), df(x₀)/dx, y', у'_x, dy/dx. Итак, по определению,

f'(x₀)= lim_Δx→0 Δx/Δy = lim_Δx→0 (f(x₀ + Δx) - f(x₀))/Δx,

Операция вычисления производной наз. дифференцированием. Если f'(х₀) - конечна, функция f(х) наз. дифференцируемой в точке х₀. Функция, дифференцируемая в каждой точке нек-рого промежутка, наз. дифференцируемой в промежутке.

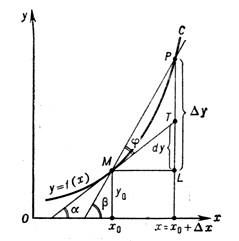
Рис. 1.

Геометрическое истолкование производной. Пусть С -плоская кривая, заданная в прямоугольной системе координат уравнением y = f(x), где f(x) определена и непрерывна в нек-ром интервале, М(х₀, у₀) - фиксированная точка на С, Р(х, у) -произвольная точка кривой С, MP - секущая (см. рис. 1). Прямая МТ наз. касательной к кривой С в точке М, если угол φ между секущей MP и этой прямой стремится к нулю, когда х → х₀ (иными словами, когда точка Р ∈ С произвольным образом стремится к точке М). Если упомянутая касательная существует, то она - единственна. Если положить x = x₀ + Δx, Δy = f(x₀ + Δх) - f(x₀), то для угла β между MP и положительным направлением оси Ох будет иметь место равенство tg β = Δx/Δy (см. рис. 1). Кривая С имеет в точке М касательную в том и только в том случае, если существует lim_Δx→0 Δx/Δy т. е. существует f'(х₀). При этом для угла α между касательной и положительным направлением оси Ох справедливо равенство tg α = f'(х₀). В случае конечной производной f'(х₀) касательная образует с Ох острый угол, т. е. -π/2 < α < π/2; в случае f'(х₀) = ∞ касательная образует с Ох прямой угол (см. рис. 2). Таким образом, производная непрерывной функции f(x) в точке х₀ совпадает с угловым коэффициентом tg α касательной к кривой, заданной уравнением у = f(x), в ее точке с абсциссой х₀.

Механическое истолкование производной. Пусть точка М движется прямолинейно по закону s = f(t). За время Δt точка М сместится на Δs = f(t + Δt) - f(t). Отношение Δs/Δt представляет собой среднюю скорость v_ср точки за время Δt. При неравномерном движении v_ср не постоянна. Мгновенной скоростью в момент t наз. предел средней скорости при Δt → 0, т. е. v = f'(t) (в предположении, что эта производная существует).

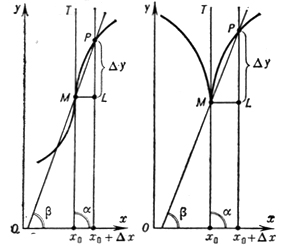
Рис. 2.

Таким образом, понятие производной доставляет общее решение задачи о построении касательной к плоской кривой и задачи о вычислении скорости прямолинейного движения. Эти две задачи явились основными предпосылками в формировании понятия производной.

Функция, имеющая в точке х₀ конечную производную, непрерывна в этой точке. В случае бесконечной производной этого может не быть. Непрерывная функция может не иметь ни конечной, ни бесконечной производной. Существуют непрерывные функции, не имеющие производной ни в одной точке области определения.

Для производных основных элементарных функций справедливы следующие формулы (в любой точке области определения; исключения оговариваются):

1) если f(х) = С = const, то f(х) = С = 0;

2) если f(х) = х, то f'(х) = 1;

3) (x^α)' = αx^α-1, α = const (х ≠ 0, если α ≤ 1);

4) (а^x)' = а^x ln a, a = const > 0, а ≠ 1, в частности, (e^x)' = e^x;

5) (log_ax)' log_ae/x = 1/xln a, a = const > 0, а ≠ 1, (ln х)' = 1/x;

6) (sin х)' = cos х;

7) (cos x)' = -sin x;

8) (tg x)' = 1/cos² x;

9) (ctg x)' = -1/sin² x;

10) (arcsin х)' = 1/√(1 - x²), х ≠ ±1;

11) (arccos x)' = -1/√(1 - x²), х ≠ ±1;

12) (arctg x)' = 1/(1 + x²);

13) (arcctg x)' = -1/(1 + x²);

14) (sh x)' = ch x;

15) (ch x)' = sh x;

16) (th x)' = 1/ch²x; 17) (cth x)' = -1/sh²x.

Имеют место также следующие правила дифференцирования;

1) Если функции u(х) и v(x) дифференцируемы в точке х₀, то функции

ċu (где с = const), u ± v, uv, u/v (v ≠ 0)

также дифференцируемы в этой точке, причем (сu)' = сu',

(u ± v)' = u' ± v', (uv)' = u'v + uv',

(u/v)' = (u'v - uv')/v²

2) Теорема о производной сложной функции: если функция y = f(u) дифференцируема в точке u₀, а функция φ(х) дифференцируема в точке х₀, причем u₀ = φ(х₀), то сложная функция y = f(φ(x)) дифференцируема в точке х₀ и y'x = f(u₀)φ'(x₀) или, в другой записи, dy/dx = dy/du du/dx.

3) Теорема о производной обратной функции: если y = f(х) и x = g(y) - две взаимно обратные возрастающие (или убывающие) функции, заданные на нек-рых интервалах, и существует конечная производная f'(х₀) ≠ 0, то в точке y₀ = f(x₀) существует конечная производная g'(у₀) = 1/f'(x₀), или, в другой записи, dx/dy = 1/(dy/dx). Эта теорема допускает обобщение: если, при выполнении прочих условий, f'(х₀) = 0(f'(х₀) = ∞), то g'(y₀) = ∞ (соответственно g'(у₀) = 0).

Односторонние производные. Если в точке х₀ существует предел

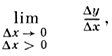
то он наз. правой производной функции y = f(x) в точке x₀ (в этом случае нет необходимости требовать, чтобы функция была определена всюду в нек-рой окрестности точки х₀; достаточно потребовать этого лишь для x ≥ x₀). Аналогично определяется левая производная - как предел

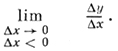
Функция f(х) имеет производную в точке х₀ в том и только в том случае, если в этой точке существуют равные между собой правая и левая производные. Для непрерывной функции существование в точке правой (соответственно левой) производной равносильно существованию в соответствующей точке ее графика правой (соответственно левой) односторонней полукасательной с угловым коэффициентом, равным значению этой односторонней производной. Точки, в к-рых полукасательные не образуют одну прямую, называются угловыми точками (см. рис. 3).

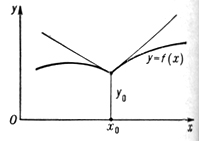
Рис. 3.

Производные высших порядков. Пусть функция y = f(x) имеет конечную производную y' = f (х) в каждой точке нек-рого интервала; эта производная наз. также первой производной, или производной первого порядка, к-рая, будучи функцией от х, может, в свою очередь, иметь производную y'' = f''(x), называемую второй производной, или производной второго порядка, функции f(x), и т.д. Вообще n-я производная, или производная порядка n, определяется по индукции равенством у⁽ⁿ⁾ = (y^(n-1))', в предположении, что y^(n-1) определена на нек-ром интервале. При этом, наряду с y⁽ⁿ⁾, используются также обозначения f⁽ⁿ⁾(х), dⁿf(x)/dxⁿ, а для n = 2, 3 еще у'', f''(x), у''', y'''(х). Вторая производная имеет механич. истолкование:

это есть ускорение w = d²s/dt² = f''(t) в момент t точки,

движущейся прямолинейно по закону s = f(t).

Дифференциал. Пусть функция y = f(x) определена в нек-рой окрестности точки х и существует такое число А, что приращение Δу может быть представлено в виде Δy = АΔх + ω, где ω/Δх → 0 при Δх → 0. Член А Δх в этой сумме обычно обозначается символом dy, или df(x), и наз. дифференциалом функции f(x) (по переменному х) в точке х. Дифференциал есть главная линейная часть приращения функции (геометрически изображается отрезком LT на рис. 1, где МТ - касательная к кривой y = f(x) в рассматриваемой точке (х₀, y₀)).

Функция y = f(x) имеет в точке х дифференциал в том и только в том случае, если она имеет в этой точке конечную производную

f'(x)= lim_Δx→0 Δy/Δx = А.

Функция, для к-рой существует дифференциал, наз. дифференцируемой в рассматриваемой точке. Таким образом, дифференцируемость функции означает одновременно и существование дифференциала, и существование конечной производной. При этом dy = df(x) = f'(x)Δx. Для независимого переменного х полагают dx= Δх и поэтому можно писать dy = f'(x)dx, т. е. производная равна отношению дифференциалов:

f'(x) = dy/dx.

См. также Дифференциал.

Формулы и правила вычисления для производных приводят к соответствующим формулам и правилам вычисления для дифференциалов. В частности, справедлива теорема о дифференциале сложной функции: если функция y = f(u) дифференцируема в точке u₀, а функция у(х) дифференцируема в точке х₀, причем u₀ = у(х₀), то сложная функция у = =f(φ(x)) дифференцируема в точке х₀ и dy = f'(u₀)du, где du = φ'(x₀)dx. Дифференциал сложной функции имеет точно такой же вид, как если бы переменное и было независимым. Это свойство наз. инвариантностью формы дифференциала. Однако, если и - независимое переменное, du = Δu есть произвольное приращение, а если u - функция, то du есть дифференциал этой функции, вообще говоря, не совпадающий с ее приращением.

Дифференциалы высших порядков. Дифференциал dy наз. также первым дифференциалом, или дифференциалом первого порядка. Пусть y = f(x) имеет дифференциал dy = f'(x)dx в каждой точке нек-рого интервала. Здесь dx = Δx - некоторое число, не зависящее от х, и поэтому можно считать dx = const. При этом dy оказывается функцией только от x и, в свою очередь, может иметь дифференциал, к-рый наз. вторым дифференциалом, или дифференциалом второго порядка функции f(x), и т. д. Вообще, n-й дифференциал, или дифференциал n-го

порядка, определяется по индукции равенством dⁿy = d(d^n-1y) в предположении, что дифференциал d^n-1y определен в нек-ром интервале и что значение dx одно и то же на всех шагах. Свойство инвариантности для d²y, d³y, вообще говоря, не имеет места (ис-

ключение составляет y = f(u), где u - линейная функция).

Повторный дифференциал от dy имеет вид

δ(dy) = f''(x)dxδx

и вторым дифференциалом является значение δ(dy) при dx = δx.

Основные теоремы и приложения Д. и. К основным теоремам Д. и. для функций одного переменного обычно относят Ролля теорему, Лагранжа теорему (о конечном приращении), Коши теорему и Тейлора формулу. Эти теоремы лежат в основе наиболее важных приложений Д. и. к исследованию свойств функций - таких, как возрастание и убывание функции, выпуклость и вогнутость графика, к отысканию экстремумов, перегиба точек, асимптот графика. Д. и. позволяет вычислять пределы функций во многих случаях, когда простейшие теоремы о пределах не позволяют сделать этого (см. Неопределенностей раскрытие). Д. и. находит широкие приложения во многих разделах математики, в частности в геометрии.

Д. и. функций многих переменных. Для простоты рассматривается случай функций двух переменных (за нек-рым исключением), хотя все понятия легко распространяются на случай трех и большего числа переменных. Пусть функция z = f(x, у) задана в нек-рой окрестности точки (х₀, у₀) и пусть зафиксировано значение у = у₀. Тогда f(x, у₀) есть функция только от х. Если она имеет в х₀ производную по х, то эта производная наз. частной производной функции f(x, у) по х в точке (х₀, у₀) и обозначается f'_x(x₀, y₀), ∂f(x₀, y₀)/∂x, ∂f/∂x, z'_x, ∂z/∂x. Итак, пo определению,

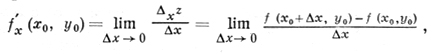
где Δ_xz = f(x₀ + Δх, y₀) - f(x₀, y₀) - частное приращение функции по х (∂z/∂x) в общем случае нельзя рассматривать как дробь; ∂/∂x есть символ операции).

Аналогично определяется частная производная по у:

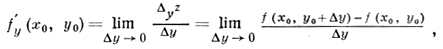
где Δ_yz - частное приращение функции по у. Другие обозначения: ∂f(x₀, y₀)/∂y, ∂f/∂y, z'_y, ∂z/∂y. Частные производные вычисляются по правилам дифференцирования функций одного переменного (при вычислении z'_x нужно считать у = const, а при вычислении z'_y -считать х= const).

Частными дифференциалами функции z = f(x, у) в точке (х₀, у₀) наз. (соответственно) выражения

d_xz = f'_x(x₀, y₀) dx; d_yz = f'_y (х₀, у₀) dy

(где, как и в случае одного переменного, dx = Δх, dy = Δy означают приращения независимых переменных).

Первые частные производные ∂z/∂x = f'_x(x, у) и ∂z/∂y = f'_y(x, у), или частные производные первого порядка, являясь функциями от х и у, могут в свою очередь иметь частные производные по х и у, к-рые называются, по отношению к функции z = f(x, у), частными производными второго порядка, или вторыми частными производными. При этом полагают

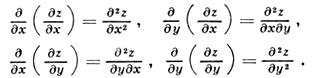
Вместо ∂²/∂x² употребляют также обозначения

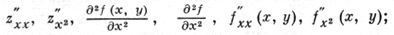
вместо ∂²z/∂x∂y - обозначения

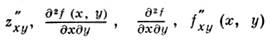
и т. д. Подобным образом вводятся частные производные третьего порядка и выше, и соответствующая символика: ∂ⁿz/∂xⁿ - функция z дифференцируется n раз по х; ∂ⁿz/∂x^p∂y^q, где n = p + q,- функция z дифференцируется р раз по х и q раз по у. Частные производные второго и высших порядков, являющиеся результатом дифференцирования по разным переменным, наз. смешанными частными производными.

Каждой частной производной отвечает нек-рый частный дифференциал, получаемый умножением ее на дифференциалы независимых переменных, взятые в степенях, равных числу дифференцирований по соответствующему переменному. Так получаются n-е частные дифференциалы, или частные дифференциалы n-го порядка:

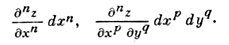
Справедлива следующая важная теорема о смешанных производных: если в нек-рой окрестности точки (х₀, у₀) функция z = f(x, у) имеет смешанные частные производные f''_xy(x, у) и f''_yx(x, у) и эти производные непрерывны в точке (х₀, у₀), то f''_xy(x₀, y₀) = f''_yx(x₀, y₀).

Функция z = f(x, у) наз. дифференцируемой в точке (х₀, у₀) по совокупности переменных х и у, если она определена в нек-рой окрестности этой точки и ее полное приращение

Δz = f(x₀ + Δx, y₀ + Δy) - f(x₀, у₀)

может быть представлено в виде

Δz = A Δx + В Δу + ω,

где А и В - некоторые числа, ω/ρ → 0 при ρ = √((Δx)² + (Δy)²)) → 0 (при условии, что точка (х₀ + Δх, у₀ + Δy) принадлежит упомянутой окрестности). При этом выражение

dz = df(x₀, у₀) = А Δх + В Δу

наз. полным дифференциалом (первого порядка) функции f(x, у) в точке (х₀, у₀); это есть главная линейная часть приращения. Функция, дифференцируемая в точке, непрерывна в этой точке (обратное не всегда верно!). Более того, дифференцируемость влечет существование конечных частных производных

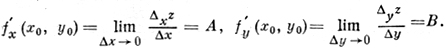
Таким образом, для функции, дифференцируемой в (x₀, y₀), dz = df(x₀, y₀) = f'_x(x₀, y₀) Δx + f'_y(х₀, у₀) Δу,

или

dz = df(x₀, y₀) = f'_x(x₀, у₀) dx + f'_y(x₀, у₀) dy,

если, подобно случаю одного переменного, положить для независимых переменных dx = Δх, dy = Δу.

Существование конечных частных производных в общем случае не влечет ее дифференцируемости (здесь нарушается аналогия с функциями одного переменного). Достаточный признак дифференцируемости функции двух переменных: если в нек-рой окрестности точки (х₀, y₀) функция f(x, у) имеет конечные частные производные f'_x(x, у) и f'_y(x, у), непрерывные в точке (х₀, y₀), то f дифференцируема в этой точке. Геометрически полный дифференциал df(x₀, y₀) есть приращение аппликаты касательной плоскости к поверхности z = f(x, у) в точке (х₀, у₀, z₀), где z₀ = f(х₀, у₀) (см; рис. 4).

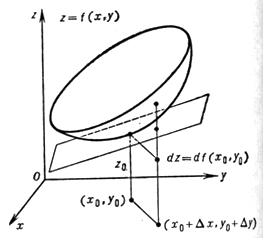
Рис. 4.

Полные дифференциалы высших порядков, подобно случаю функций одного переменного, вводятся по индукции равенством

dⁿz = d(d^n-1 z)

в предположении, что дифференциал d^n-1z определен в нек-рой окрестности рассматриваемой точки и что приращения аргументов dx, dy берутся одни и те же на всех шагах. Аналогично определяются и повторные дифференциалы.

Производные и дифференциалы сложных функций. Пусть w = f(u₁, ..., u_m) - функция m переменных, дифференцируемая в каждой точке открытой области D m-мерного евклидова пространства R^m, и пусть m функций u₁ = φ₁(х₁, ..., х_n), ..., u_m = φ_m(x₁, ..., х_n) - от n переменных заданы в открытой области G n-мерного евклидова пространства Rⁿ. Пусть, наконец, точка (u₁, ..., u_m), соответствующая точке (х₁, ..., x_n) ∈ G, не выходит из области D. Тогда справедливы следующие теоремы:

1) Если функции φ₁, ..., φ_m имеют конечные частные производные по х₁, ..., х_n, то сложная функция w = f(u₁, ..., u_m) от х₁, ..., х_n также имеет конечные частные производные по х₁, ..., х_n и

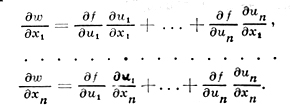
2) Если функции φ₁, ..., φ_m дифференцируемы по совокупности переменных x₁ ..., х_n в точке (x₁ ..., х_n) ∈ G, то и сложная функция w = f(u₁ ..., u_m) дифференцируема в этой точке и

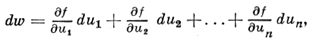
где du₁ ..., du_m - дифференциалы функций u₁ ..., u_m. Таким образом, свойство инвариантности первого дифференциала имеет место и для функций нескольких переменных. Для дифференциалов второго и высших порядков это свойство, вообще говоря, нарушается.

Д. и. применяется к изучению свойств функций многих переменных: к отысканию экстремумов, к исследованию функций, задаваемых одним или несколькими неявными уравнениями, к теории поверхностей и т. д. Одним из главных инструментов при этом является Тейлора формула.

Понятия производной и дифференциала и их простейшие свойства, связанные с арифметич. действиями над функциями и суперпозицией функций, включая свойство инвариантности первого дифференциала, почти без изменений распространяются на комплексные функции одного или нескольких действительных переменных, на действительные и комплексные вектор-функции одного или нескольких действительных переменных, на комплексные функции и вектор-функции одного или нескольких комплексных переменных. В функциональном анализе понятия производной и дифференциала распространяются на функции точки абстрактного пространства.

Лит.: История дифференциального и интегрального исчисления - [1] История математики с древнейших времен до начала XIX столетия, т. 1-3, М., 1970-72; [2] Рыбников К. А., История математики, т. 1-2,М., 1960-63; [3] Вилейтнер Г., История математики от Декарта до середины XIX столетия, пер. с нем., 2 изд., М., 1966; [4] Стройк Д. Я., Краткий курс истории математики, пер. с нем., 2 изд., М., 1969; [5] Бурбаки Н., Очерки по истории математики, пер. с франц., М., 1963; [6] Сantоr М., Yorlesungén über Geschichte der Mathematik, 2 Aufl., Bd 1-4, Lpz., 1900-08.

Работы основоположников и классиков дифференциального и интегрального исчисления - [7] Ньютон И., Математические работы, пер. с латин., М.- Л., 1937; [8] Лейбниц Г., Избранные отрывки из математических сочинений, пер. с латин., «Успехи матем. наук», 1948, т. 3, в. 1; [9] Л'Опиталь Г. Ф. де, Анализ бесконечно малых, пер. с франц., М.- Л., 1935; [10] Эйлер Л., Введение в анализ бесконечных, пер. с латин., 2 изд., т. 1, М., 1961; [11] его же, Дифференциальное исчисление, пер. с латин., М.-Л., 1949; [12] Коши О. Л., Краткое изложение уроков о дифференциальном и интегральном исчислении, пер. с франц., СПБ, 1831; [13] его же, Алгебраический анализ, пер. с франц., Лейпциг. 1864.

Учебники и учебные пособия по дифференциальному и интегральному исчислению - [14] Гурса Э., Курс математического анализа, пер. с франц., 3 изд., т. 1, М.-Л., 1936; [15] Ла Балле Пуссен Ш. Ж. де, Kvpc анализа бесконечно малых, пер. с франц., т. 1, Л.-М., 1933; [16] Курант Р., Курс дифференциального и интегрального исчисления, пер. с нем. и англ., 4 изд., т. 1, М., 1967; [17] Рудин Р., Основы математического анализа, пер. с англ., М., 1966; [18] Ильин В. А., Позняк Э. Г., Основы математического анализа, т. 1, 3 изд., М., 1971; т. 2, 1973; [19] Кудрявцев Л. Д., Математический анализ, 2 изд., М., 1973; [20] Никольский С. М., Курс математического анализа, 2 изд., М., 1975; [21] Толстов Г. П., Элементы математического анализа, т. 1-2, 2 изд., М., 1974; [22] Смирнов В. И., Курс высшей математики, 22 изд., т. 1, М., 1967; [23] Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., М., 1969; [24] Xинчин А. Я., Восемь лекций по математическому анализу, 3 изд., М-Л., 1948.

Г. П. Толстов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.