ДИФФЕРЕНЦИАЛЬНАЯ ЭНТРОПИЯ

ДИФФЕРЕНЦИАЛЬНАЯ ЭНТРОПИЯ - формальный аналог понятия энтропии для случайных величин, имеющих плотность распределения. Д. э. случай-ной величины ξ, определенной на нек-ром вероятностном пространстве (Ω 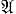, Р), принимающей значения в n-мерном евклидовом пространстве ℝⁿ и имеющей плотность распределения р(х), x ∈ ℝⁿ, дается формулой

h(ξ) = ℚ_ℝⁿ p(x) log p(x) dx

(здесь 0log0 считается равным 0). Таким образом, Д. э. совпадает с энтропией меры Р(⋅) относительно меры Лебега λ(⋅), где Р(⋅) - распределение ξ.

Понятие Д. э. оказывается полезным при вычислении различных теоретико-информационных характеристик, в первую очередь информации количества J(ξ, η) случайных векторов ξ и η. В случае, когда h(ξ), h(η) и h(ξ, η) (Д. э. пары (ξ, η)) конечны, справедлива формула:

J(ξ, η) = -h(ξ, η) + h(ξ) + h(η).

Среди свойств Д. э. можно отметить следующие два: 1) в отличие от обычной энтропии, Д. э. не ковариантна относительно изменения системы координат и может принимать отрицательные значения; 2) пусть φ(ξ) - дискретизация с шагом Δх n-мерной случайной величины ξ, обладающей плотностью, тогда для энтропии H(φ(ξ)) справедлива формула

H(φ(ξ)) = -n logΔx + h(ξ) + o (1)

при Δх → 0. Таким образом, Н(φ(х)) → +∞ при Δх → 0, главный член асимптотики H(φ(ξ)) зависит от размерности пространства значений ξ, Д. э. задает следующий по порядку член асимптотич. разложения, не зависящий от Δх, причем это первый член, в к-ром проявляется зависимость от конкретного вида распределения ξ.

Лит.: [1] Гельфанд И. М., Колмогоров А. Н., Яглом А. М., в кн.: Тр. 3-го Всесоюзного математического съезда, т. 3, М., 1958, с. 300 - 320; [2] Rénуi A., Wahrscheinlichkeitsrechnung, В., 1962.

Р. Л. Добрушин, В. В. Прелов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.