ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА

ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА - 1) Д. ф. степени р, р-форма на дифференцируемом многообразии М - р раз ковариантное тензорное поле на М. Ее можно интерпретировать также как р-линейное (над алгеброй F(M) гладких вещественных функций на М) отображение X(М)Р → F(M), где X(М) есть F(М)-модуль гладких векторных полей на М. Формы степени 1 наз. также пфаффовыми формами. Примером такой формы является дифференциал df гладкой функции f на М, определяемый следующим образом: (df)(X), X ∈ X(М), есть производная Xf функции f по направлению поля X. Римановы метрики на многообразии М служат примерами симметрических Д. ф. степени 2. Часто, однако, термин «Д. ф.» относят к кососимметрическим, или внешним Д. ф., имеющим наибольшее число приложений.

Если (x¹, ..., хⁿ) - локальная система координат

в области U ⊂ M, то формы dx¹, ..., dxⁿ составляют базис в кокасательном пространстве Т_x(М)*, x ∈ U. Поэтому (см. Внешняя алгебра) любая внешняя р-форма α записывается в U в виде

∑_i1,...,ip a_i1,...,ip dx^i₁ ∧ ... ∧ dx^i_p, (1)

где a_i1,...,ip - функции в U. В частности,

df = ∂f/∂xⁱ dxⁱ.

Пусть Е^p = Е^p(М) - пространство всех внешних р-форм класса С^∞, причем Е⁰(М) = F(M). Внешнее умножение α × β превращает Е*(M)=∑ⁿ_p=0 Е^p(М) (где

n = dim М) в ассоциативную градуированную алгебру над F(M), удовлетворяющую условию градуированной коммутативности

α ∧ β = (-1)^p_q β ∧ α, α ∈ Е^p, β ∈ E^q. (2)

Гладкое отображение многообразий f: М → А порождает гомоморфизм f* : Е* (N) → E*(М) алгебр над ℝ.

Понятие дифференциала функции обобщается следующим образом. Для всякого р ≥ 0 существует единственное линейное отображение d : Е^p → Е^p+1 (внешний дифференциал), совпадающее при р = 0 с введенным выше дифференциалом и обладающее свойствами:

d(α ∧ β) = dα ∧ β + (-1)^p α ∧ dβ, α ∈ Е^p, β ∈ E^q, d(dα) = 0.

Внешний дифференциал формы α, записанной в локальных координатах в виде (1), выражается формулой

dα = ∑_i1,...,ip da_i1,...,ip ∧ dx^i₁ ∧ ... ∧ dx^i_p.

Его бескоординатная запись:

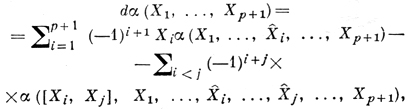
где Х₁, ..., Х_p+1 ∈ X(М). Оператор взятия Ли производной L_X, X(М), на Д. ф. связан с внешним дифференциалом соотношением

L_X = d ○ ι_X + ι_X ○ d,

где ι_X : Е^p → Е^p-1 - оператор внутреннего умножения на X:

(ι_Xα) (Х₁, ..., X_p-1) = α(Х, X₁, Х_p-1), α ∈ Е^p(М), X₁, Х_p-1 ∈ X(М).

Оператор d превращает Е*(М) в коцепной комплекс (комплекс де Рама). Коциклы этого комплекса наз. замкнутыми формами, кограницы - точными формами. Согласно де Рама теореме, алгебра когомологий

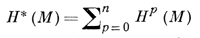
комплекса де Рама изоморфна алгебре Н*(М, ℝ) вещественных когомологий многообразия М. В частности, Н^p(ℝⁿ) = 0 при р > 0 (лемма Пуанкаре).

С теоремой де Рама тесно связана другая операция - интегрирование Д. ф. Пусть D - ограниченная область в ℝ^p, s - гладкое отображение ℝⁿ → M, определенное в окрестности замыкания D. Если α ∈ Е^p(М), то s*α = adx¹ ℙ ... ∧ dx^p, где а - гладкая функция в D̅. Интеграл формы α по поверхности s определяется формулой

∫_sα = ∫_D а(х₁, ..., x_p) dx¹ ... dx^p.

Если D имеет кусочно гладкую границу, то справедлива формула

∫_s dα = ∫_∂s α, α ∈ Е^p-1(М), (3)

где ∫_∂s α определяется как сумма интегралов формы α

по гладким кускам границы, снабженных естественными параметризациями. Частными случаями этой формулы являются классич. формулы Ньютона -Лейбница, Грина, Гаусса - Остроградского, Стокса (см. также Стокса теорема). В силу формулы (3) каждая замкнутая р-форма α определяет р-мерный сингулярный коцикл, значение к-рого на симплексе s

равно ∫_s α Это соответствие как раз и реализует изоморфизм из теоремы де Рама.

Формула (3) была опубликована в 1899 А. Пуанкаре (см. [2]), к-рый рассматривал внешние формы как подинтегральные выражения для образования интегральных инвариантов. Одновременно Э. Картан (см. [3]) дал близкое к современному определение внешних форм и внешнего дифференциала (вначале на пфаффовых формах), подчеркнув связь своей конструкции с внешней алгеброй.

Наряду с определенными выше скалярными внешними формами можно рассматривать внешние Д. ф. со значениями в векторном пространстве V над ℝ. Если V является алгеброй, то в пространстве Е(М, V) форм со значениями в V определено естественное умножение (обобщение внешнего умножения). Если при этом алгебра V ассоциативна, то и Е(М, V) ассоциативна; если V коммутативна, то Е(М, V) градуированно-коммутативна (формула (2)); если V - алгебра Ли, то Е(М, V) - градуированная алгебра Ли. Часто рассматривается также следующее, еще более общее понятие. Пусть F - гладкое векторное расслоенное пространство с базой М. Если сопоставить каждой точке х ∈ М кососимметрическую р-линейную функцию на Т_x(М) со значениями в слое F_x расслоения F, то получится так наз. F-значная р-форма. F-значную р-форму можно интерпретировать также как р-линейное (над F(M)) отображение модуля X(М)^p в модуль гладких сечений расслоения F. Пространство таких форм обозначается E^p(F). Если F задано локально постоянными функциями перехода или, что то же, в F задана плоская связность, то можно корректно определить комплекс де Рама и обобщить теорему де Рама на этот случай.

Формы со значениями в касательном расслоении Т(М) наз. также векторными Д. ф.; векторные р-формы можно отождествить с р раз ковариантными и 1 раз контравариантными тензорными полями на М, кососимметрииными по ковариантным индексам. С помощью векторных Д. ф. описываются дифференцирования алгебры внешних форм Е(М) [4]. Векторные формы (а также их обобщение - струйные формы) находят применение в теории деформаций комплексных и других дифференциально-геометрич. структур на многообразиях.

Аналоги Д. ф. можно построить также в симплициальной теории. Одна из таких конструкций, восходящая к X. Уитни [5], может быть использована для вычисления рациональных когомологий симплициального комплекса K. Кусочно линейной формой (или PL - формой) на K наз. согласованный набор Д. ф., заданных на симплексах комплекса K и имеющих в качестве коэффициентов при записи в барицентрич. координатах многочлены с рациональными коэффициентами. PL-формы на K образуют градуированно-коммутативную дифференциальную алгебру E*_PL(K) над ℚ. Интегрирование форм определяет изоморфизм алгебры когомологий этой алгебры на алгебру Н*(|K|, ℚ), где |K| - полиэдр, отвечающий комплексу K. Алгебра E*_PL(K) полностью определяет также рациональный гомотопич. тип (в частности, ранги гомотопич. групп) пространства |K|. Аналогично алгебра Е*(М) на дифференцируемом многообразии М определяет его вещественный гомотопич. тип [9].

Исчисление внешних форм на комплексном аналитич. многообразии имеет ряд особенностей [6]. В этой ситуации обычно рассматриваются пространства Е^p(М, ℂ) комплекснозначных форм или пространства E^p(F), где F - голоморфное векторное расслоение на М. Имеет место разложение

Е^p(М, ℂ) = ∑_r+s=p E^r,s(M),

где E^r,s(M) - пространство форм типа (r, s), т. е. форм α, локально представимых в виде

∑ a_{i1,...,ir, j1,...,js} dz^i₁ ∧ ... ∧ dz^i_r ∧ dz̅^j₁ ∧ ... ∧ dz̅^j_s,

где (z¹, zⁿ) - локальная аналития. система координат на М. Аналогично

E^p(F) = ∑_r+s=p E^r,s(F).

Далее, d = d' + d'', где

d: E^r,s(М) → E^r+1,s(М), d'': E^r,s(M) → E^r,s+1(M).

При этом d'² = d''² = 0, так что d' и d'' определяют коцепные комплексы. Наиболее известен комплекс оператора d'' (комплекс Дольбо), когомологии к-рого обозначаются через H^r,s(M). d''-коциклы типа (р, 0) суть голоморфные р-формы (см. Голоморфная форма). Для d'' справедлива следующая лемма Гротендика: если α - форма типа (r, s) с s > 0 в окрестности нуля пространства ℂⁿ и d''α = 0, то в меньшей окрестности нуля существует такая форма β типа (r, s-1), что α = d''β. Комплекс Дольбо можно определить также и для F-значных форм, где F - голоморфное векторное расслоение. Это приводит к пространствам когомологий H^r,s(F). Из леммы Гротендика вытекает следующий изоморфизм:

H^r,s(F) ≅ H^s(М, Ω^r(F)),

где Ω^r(F) - пучок ростков голоморфных F-значных r-форм (теорема Дольбо). В частности,

H^r,s(M) ≅ H^s(М, Ω^r(М)),

где Ω^r(M) - пучок ростков голоморфных r-форм на М. Существует спектральная последовательность с первым членом Σ_r,s H^r,s(М), сходящаяся к Н*(М, ℂ). Эйлерова характеристика χ(М) компактного комплексного многообразия М выражается через когомологий Дольбо по формуле

χ(М) = ∑_r,s (-1)^r+s dim H^r,s(M).

Д. ф. являются важной составной частью аппарата дифференциальной геометрии (см. [7], [8]). Они систематически используются также в топологии, теории дифференциальных уравнений, механике, теории комплексных многообразий и функций многих комплексных переменных. Обобщением Д. ф., аналогичным обобщенным функциям, являются потоки. Алгебраич. аналог теории Д. ф. (см. Дифференциалов модуль) позволяет определить дифференциальные формы на алгебраических многообразиях и на аналитических пространствах (см. Дифференциальное исчисление на аналитических пространствах). См. также Рама когомологий, Дифференциал на римановой поверхности, Гармоническая форма, Голоморфная форма, Лапласа оператор.

Лит.: [1] де Рам Ж., Дифференцируемые многообразия, пер. с франц., М., 1956; [2] Poincaré Н., Les methodes nouvelles de la mécanique céleste, t. 3, P., 1899; [3] Саrtan E., Œuvres complètes, pt. 2, t. 1, p. 303-96; [4] Fröliсher A., Nijenhuis A.,«Proc. Koninkl. ned. akad. wet.», Ser. A, 1956, v. 59, № 3, p. 338-59; [5] Уитни X., Геометрическая теория интегрирования, пер. с англ., М., 1960; [6] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976; [7] Стернберг С., Лекции по дифференциальной геометрии, пер. с англ., М., 1970; [8] Картан А., Дифференциальное исчисление. Дифференциальные формы, пер. с франц., М., 1971; [9] Гриффите Ф. [и др.], «Успехи матем. наук», 1977, т. 32, в. 3, с. 119-52.

А. Л. Онищик.

2) Д. ф. на алгебраическом многообразии - аналог понятия дифференциальной формы на дифференцируемом многообразии. Пусть X -неприводимое алгебраич. многообразие размерности d над алгебраически замкнутым полем k, К - его поле рациональных функций. Дифференциальной формой степени r на X наз. элемент K-пространства

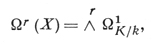
где Ω_K/k - дифференциалов модуль поля K над полем k. Если х₁, ..., x_d - сепарабельный базис трансцендентности расширения К/k, то каждая Д. ф. ω ∈ Ω^r(X) записывается в виде

ω = ∑ a_i1,...,ir dx_i1 ∧ ... ∧ dx_ir,

где a_i1,...,ir ∈ K. Д. ф. ω наз. регулярной на открытом множестве U ⊂ X, если ω принадлежит подмодулю Ω^r_k[U]/k пространства Ω^r(X), рассматриваемого как модуль над кольцом k[U] регулярных функций на подмножестве U. Д. ф. ω наз. регулярной, если любая точка х ∈ Х имеет такую окрестность U, что ω регулярна на U. Регулярные Д. ф. на X образуют модуль над k[Х], обозначаемый Ω^r[X]. Его элементы отождествляются с сечениями пучка Ω^r_X/k на многообразии X. В окрестности любой точки х ∈ Х регулярная Д. ф. ω ∈ Ω^r[X] записывается в виде

ω = ∑ α_i1,...,ir df_i1 ∧ ... ∧ df_i1, где функции α_i1,...,ir df_i1, ..., df_i1 регулярны в точке х. Если X - полное многообразие, то пространства Ω^r[Х] конечномерны, а в случае, когда X неособое, размерность p_g(X) = dim_k Ω^d[X] наз. геометрическим родом многообразия X. В случае, когда X - полное многообразие над полем комплексных чисел, пространство Ω^r[Х] совпадает с пространством голоморфных Д. ф. степени r на соответствующем аналитич. пространстве Х^an.

Пусть X - нормальное многообразие и ω ∈ Ω^d[Х]; для любой точки х ∈ Х⁽¹⁾ коразмерности 1 Д. ф. ω может быть записана в виде

ω' = a dt ∧ dt₁ ∧ ... ∧ dt_d-1, (*)

где а принадлежит полю частных К_x локального кольца 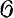_X,x, t - образующая его максимального идеала, t₁, ..., t_d-1 - сепарабельный базис трансцендентности над k поля вычетов кольца 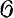_X,x. Значение нормирования на элементе а, определяемое кольцом 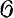_X,x, не зависит от выбора представления ω в виде (*) и обозначается ν_x(ω). Дивизор

D = ∑_{x∈X⁽¹⁾} ν_x(ω) {x̅}

определен и наз. дивизором дифференциальной формы ω. Д. ф. ω регулярна тогда и только тогда, когда ее дивизор D ≥ 0, т. е. ν_x(ω) ≥ 0 для всех x ∈ Х. Дивизоры любых двух Д. ф. эквивалентны, более того, дивизоры всех Д. ф. на данном алгебраич. многообразии образуют класс дивизоров относительно линейной эквивалентности. Этот класс наз. каноническим классом многообразия X и обозначается через К_X. Для неособого многообразия X класс К_X совпадает с первым классом Чженя обратимого пучка Ω^d_X/k, в частности

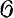Ω^d_X/k ≃ _X(D)

для любого D ∈ К_X.

Для любого доминантного рационального отображения алгебраич. многообразий f: X' → X определен канонич. гомоморфизм

f*: Ω^r(X) → Ω^r(X').

При этом, если X и X' - неособые, а X - полное, то f* переводит регулярные Д. ф. в регулярные. В частности, если неособые полные многообразия X и X' бирационально изоморфны, то векторные пространства Ω^r[Х] и Ω^r[X'] изоморфны над полем k.

Для любого i > 1 элементы i-й симметрич. степени Sⁱ(Ω^r(X)) K-пространства Ω^r(X) наз. i-кратными дифференциальными формами степени r на X. Каждую такую Д. ф. можно рассматривать как рациональное сечение пучка S'(Ω^r_X/k). Регулярные сечения

ω ∈ Г(X, Sⁱ(Ω^r_X/k))

наз. регулярными i-кратными дифференциальными формами степени r на X. Для неособого полного многообразия X размерность

P_i(X) = dim_k Г(X, Sⁱ(Ω^d_X/k))

наз. i-родом многообразия X. Для бирационально изоморфных многообразий их i-роды совпадают.

Лит.: [1] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972; [2] Бальдассарри М., Алгебраические многообразия, пер. с англ., М., 1961.

И. В. Долгачев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.