ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ - раздел геометрии, в к-ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в Д. г. изучаются свойства семейств линий и поверхностей (см., напр., Конгруэнция, Сеть).

Д. г. возникла и развивалась в тесной связи с математич. анализом, к-рый сам в значительной степени вырос из задач геометрии. Многие геометрич. понятия предшествовали соответствующим понятиям анализа. Так, напр., понятие касательной предшествовало понятию производной, понятие площади и объема -понятию интеграла.

Возникновение Д. г. относится к 18 в. и связано с именами Л. Эйлера (L. Euler) и Г. Монжа (G. Monge). Первое сводное сочинение по теории поверхностей написано Г. Монжем (Приложение анализа к геометрии, 1795). В 1827 К. Гаусс (С. Gauss) опубликовал работу «Общее исследование о кривых поверхностях», в к-рой заложил основы теории поверхностей в ее современном виде. С тех пор Д. г. перестала быть только приложением анализа и заняла самостоятельное место в математике.

Открытие в 1826 Н. И. Лобачевским неевклидовой геометрии сыграло огромную роль в развитии всей геометрии, в том числе и Д. г. Фактически Н. И. Лобачевским было отвергнуто априорное представление о пространстве, господствовавшее ранее в математике и философии. Он открыл, что возможны пространства, отличные от евклидова. Эта идея Н. И. Лобачевского нашла отражение в различных математич. исследованиях. Так, в 1854 Б. Риман (В. Riemann) своей лекцией «О гипотезах, лежащих в основаниях геометрии» заложил основы римановой геометрии, к-рая в применении к многомерным многообразиям находится в таком же отношении к геометрии n-мерного пространства, как внутренняя геометрия поверхности к евклидовой геометрии на плоскости.

Теоретико-групповая точка зрения Ф. Клейна (F. Klein), изложенная в его «Эрлангенской программе» (1872), т. е.: геометрия - учение об инвариантах групп преобразований, в применении к Д. г. была развита Э. Картаном (Е. Cartan), к-рый построил теорию пространств проективной связности и аффинной связности.

В России школу Д. г. создали Ф. Миндинг и К. М. Петерсон. Их исследования посвящены в значительной степени вопросам изгибания поверхностей, т. е. таким непрерывным деформациям поверхностей, при которых внутренняя геометрия все время остается неизменной. Эти исследования были продолжены в работах многих русских и советских геометров.

Теория кривых. В теории кривых обычно рассматривают так наз. регулярные кривые. Это - кривые, допускающие локальное задание уравнениями вида

x = x(t), y = y(t), z = z(t), (1)

где x(t), y(t), z(t) - достаточно регулярные функции параметра t. В зависимости от свойств дифференцируемости функций x(t), y(t), z(t), задающих кривую, говорят о степени регулярности кривой. Кривая допускает бесчисленное множество различных способов параметрич. задания уравнениями вида (1). Среди них особое значение имеют так наз. естественная параметризация, когда параметром служит длина дуги кривой, отсчитываемая от нек-рой фиксированной точки. Точка кривой наз. обыкновенной, если при подходящем выборе прямоугольной декартовой системы координат х, у, z она допускает в окрестности этой точки задание уравнениями вида

у = у(х), z = z(x),

где у(х) и z(x) - дифференцируемые функции. В противном случае точка наз. особой (см. Особая точка). В Д. г. основное изучение кривой относится к окрестности обыкновенной точки. Для того чтобы точка кривой, заданной общим уравнением (1), была обыкновенной, достаточно, чтобы в этой точке было

х'² + у'² + z'² ≠ 0.

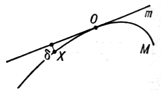
Рис. 1.

Ряд основных понятий теории кривых вводится с помощью понятия соприкосновения множеств, к-рое состоит в следующем. Пусть М и m -два множества с общей точкой О. Говорят, что множество М имеет с m в точке O соприкосновение порядка α ≥ 1, если

δ(X)/|XO|^α → 0

при Х → O, где δ(Х) - расстояние точки X множества М от m. Если в качестве М взять кривую, а в качестве m прямую, проходящую через точку О кривой, то при α ≥ 1 условие соприкосновения определяет касательную к кривой в точке О (рис. 1). Гладкая (дифференцируемая) кривая в каждой точке имеет определенную касательную. Направление касательной в точке t₀ кривой, задаваемой уравнениями (1), совпадает с направлением вектора [х'(t₀), у'(t₀), z'(t₀)]. В Д. г. выводятся уравнения касательной для различных способов аналитич. задания кривой. В частности, для кривой, задаваемой уравнениями (1), уравнения касательной в точке, отвечающей значению параметра t₀, будут

(X - x₀)/x'₀ = (Y - y₀)/y'₀ = (Z - z₀)/z'₀

где индекс ₀ указывает на значение функций х, у, z и их производных в точке t₀. Если взять в качестве m плоскость, проходящую через точку О кривой М, то условие соприкосновения при α ≥ 2 определяет

соприкасающуюся плоскость кривой (рис. 2). Дважды дифференцируемая кривая в каждой точке имеет соприкасающуюся плоскость. Она либо единственная, либо любая плоскость, проходящая через касательную кривой, является соприкасающейся.

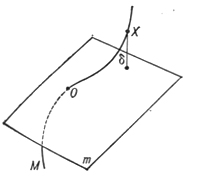
Рис. 2.

При движении вдоль кривой ее касательная вращается. Скорость этого вращения при равномерном, с единичной скоростью, движении вдоль кривой наз. кривизной кривой. В случае параметрич. задания кривой уравнениями (1) кривизна кривой определяется по формуле

k₁ = |r'(t) × r''(t)|/|r'(t)|^3/2,

где r(t) - вектор-функция с координатами x(t), y(t), z(t). Прямые и только прямые имеют всюду равную нулю кривизну. Дважды дифференцируемая кривая в каждой точке, где кривизна отлична от нуля, имеет единственную соприкасающуюся плоскость. При движении вдоль кривой в окрестности такой точки соприкасающаяся плоскость вращается, причем касательная кривой является мгновенной осью этого вращения. Скорость вращения соприкасающейся плоскости при равномерном, с единичной скоростью, движении вдоль кривой наз. кручением кривой. В зависимости от направления вращения определяется знак кручения. Трижды дифференцируемая кривая в каждой точке с отличной от нуля кривизной имеет определенное кручение. В случае параметрич. задания кривой уравнениями (1) кручение кривой определяется по формуле

k₂ = (r', r'', r''')/|r' × r''|².

Плоская кривая в каждой точке имеет кручение, равное нулю. Обратно, кривая с тождественно равным нулю кручением - плоская.

Прямая, перпендикулярная касательной, проходящая через точку касания, наз. нормалью к кривой. Нормаль, лежащую в соприкасающейся плоскости, наз. главной нормалью, а нормаль, перпендикулярную соприкасающейся плоскости, наз. бинормалью. Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, наз. естественным трехгранником (трехгранником Френе). Если ребра естественного трехгранника в данной точке кривой принять за оси прямоугольной декартовой системы координат, то уравнение кривой в естественной параметризации имеет в окрестности этой точки вид

x = s + ..., y = k₁/2 s² + ..., z =-k₁k₂/6 s³ + ...,

где k₁ и k₂ - кривизна и кручение кривой в указанной точке. На рис. 3 изображены проекции кривой на грани естественного трехгранника вблизи точки с отличными от нуля кривизной и кручением.

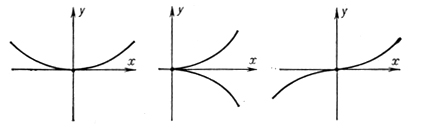
Рис. 3.

Единичные векторы τ, ν, β касательной, главной нормали и бинормали кривой при движении вдоль кривой изменяются. При соответствующем выборе направления этих векторов из определения кривизны и кручения получаются формулы

τ' = k₁ν, β' = k₂ν, ν' =- k₁τ - k₂β, (2)

где штрихом обозначено дифференцирование по дуге кривой. Формулы (2) наз. Френе формулами. Кривая с отличной от нуля кривизной определяется с точностью до положения в пространстве заданием ее кривизны и кручения в функции дуги s кривой. В связи с этим систему уравнений

k₁ = k₁(s), k₂ = k₂(s)

наз. натуральными уравнениями кривой.

Важный класс кривых представляют плоские кривые, т. е. кривые, лежащие в плоскости. Для плоских кривых можно различать направление вращения касательной при движении вдоль кривой, поэтому кривизне можно приписывать знак в зависимости от направления этого вращения. Кривизна плоской кривой, задаваемой уравнениями x = x(t), y = y(t), определяется по формуле

k = ± (y''x' - x''y')/(x'² + y'²)^3/2,

Знак + или - берется по соглашению, но сохраняется вдоль всей кривой. Для кривых вводится важное понятие соприкасающейся окружности. Это - окружность, имеющая с кривой соприкосновение порядка α ≥ 2 (рис. 4). Она существует в каждой точке дважды дифференцируемой кривой с отличной от нуля кривизной. Центр соприкасающейся окружности наз. центром кривизны, а радиус - радиусом кривизны. Радиус кривизны является величиной, обратной кривизне. Геометрич. место центров кривизны кривой наз. эволютой. Кривая, ортогонально пересекающая касательные кривой, наз. эвольвентой (рис. 5). Для эвольвенты данной кривой эволютой является сама кривая.

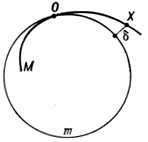
Рис. 4.

Рис. 5.

Кривая γ наз. огибающей семейства кривых γ_α, зависящих от параметра α, если она в каждой своей точке касается хотя бы одной кривой семейства и каждым своим отрезком касается бесконеяного множества этих кривых.

Теория поверхностей и ее обобщения. В теории поверхностей обычно рассматриваются регулярные поверхности. Это -поверхности, допускающие локальное задание уравнениями вида

х = х(u, v), у = у(u, v), z = z(u, v), (3)

где х(u, v), у(u, у), z(u, v) - регулярные функции параметров u, v. В зависимости от степени регулярности функций, входящих в уравнения поверхности, говорят о степени регулярности поверхности. Поверхность допускает бесчисленное множество способов параметрич. задания уравнениями вида (3). Точка поверхности наз. обыкновенной, если в ее окрестности при подходящем выборе системы координат х, у, z поверхность допускает задание вида z = z(x, у),

где z(x, у) - гладкая функция. В противном случае точка поверхности наз. особой. В Д. г. основное изучение поверхности ведется в окрестности обыкновенных точек. Для того чтобы точка (u₀, v₀) поверхности, задаваемой уравнениями (3), была обыкновенной, достаточно, чтобы в этой точке ранг матрицы

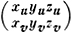
был равен двум. Когда поверхность задается уравнениями вида (3), это условие обычно предполагается выполненным и специально не оговаривается. Уравнения (3) при фиксированном u или v задают кривые, лежащие на поверхности. Эти кривые наз. координатными линиями на поверхности. Параметры u, v наз. координатами на поверхности или гауссовыми криволинейными координатами.

Через понятие соприкосновения определяется касательная плоскость к поверхности. Это - плоскость, проходящая через точку поверхности и имеющая в этой точке с поверхностью соприкосновение порядка 1. Гладкая (дифференцируемая) поверхность имеет в каждой тояке единственную касательную плоскость. Касательная плоскость поверхности, задаваемой уравнениями (3), при условии (4) в точке (u₀, v₀) определяется уравнением

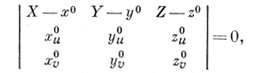
где индекс 0 указывает на значение функций х(u, v), y(u, v), z(u, v) и их производных в точке (u₀, v₀). Прямая, проходящая через точку поверхности перпендикулярно касательной плоскости в этой точке, наз. нормалью к поверхности. Если r(u, v) - вектор с координатами х(u, v), у(u, v), z(u, v), то

r_u × r_v

имеет направление нормали поверхности.

Для поверхностей вводится важное понятие соприкасающегося параболоида. Это - параболоид, для к-рого нормаль к поверхности в данной точке является его осью и к-рый имеет соприкосновение порядка α ≥ 2 с поверхностью в этой точке. В каждой точке дважды дифференцируемой поверхности существует единственный соприкасающийся параболоид, к-рый может вырождаться в параболич. цилиндр или плоскость. Если поверхность отнести к прямоугольным декартовым координатам, приняв данную точку поверхности за начало координат, а касательную плоскость в ней за плоскость ху, то уравнение поверхности в окрестности точки касания будет

z = f(x, у),

а уравнение соприкасающегося параболоида в этой точке

z = 1/2 (f_xxx² + 2f_xyxy + f_yy²)

(производные функции f берутся в точке касания). В зависимости от вида соприкасающегося параболоида точки поверхности подразделяются на эллиптические точки, гиперболические точки, параболические точки и уплощения точки. Значение соприкасающегося параболоида состоит в том, что он воспроизводит форму поверхности с точностью до бесконечно малых 2-го порядка (касательная плоскость воспроизводит ее форму с точностью до бесконечно малых 1-го порядка).

С помощью соприкасающегося параболоида вводится понятие сопряженных направлений на поверхности. Именно два направления на поверхности в данной точке наз. сопряженными, если содержащие их прямые сопряжены относительно соприкасающегося параболоида в этой точке. Ортогональные сопряженные направления наз. главными. В данной точке поверхности, как правило, два главных направления. Исключение составляют точки уплощения и специальные эллиптич. точки (округления точки), в к-рых каждое направление главное. Линия, у к-рой в каждой точке направление является главным, наз. кривизны линией. В точках поверхности, не являющихся эллиптическими, существуют самосопряженные направления. Они наз. асимптотическими направлениями. Линия на поверхности, направление к-рой в каждой точке асимптотическое, наз. асимптотической линией.

Подобно тому, как для семейства кривых на плоскости, вводится понятие огибающей семейства поверхностей. При этом семейство поверхностей может быть однопараметрическим или двухпараметрическим. В теории поверхностей особое значение имеет огибающая однопараметрич. семейства плоскостей.

В теории поверхностей важную роль играют две дифференциальные квадратичные формы поверхности, связанные с поверхностью. Если через r(u, v) обозначить вектор точки на поверхности, а через n(u, v) единичный вектор нормали к поверхности, то эти квадратичные формы записываются в виде

I = dr², II =-dr dn.

Коэффициенты первой и второй квадратичных форм обычно обозначаются Е, 2F, G и L, 2М, N соответственно. Первая из этих форм дает расстояние на поверхности между точкой (u, v) и бесконечно близкой точкой (u + du, v + dv):

ds= √(Е du² + 2F du dv + G dv²).

Длина кривой, задаваемой на поверхности уравнениями u = u(t), v = v(t), вычисляется при помощи первой квадратичной формы

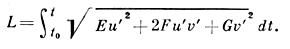
Первая квадратичная форма поверхности определяет углы между кривыми на поверхности. В частности, для угла 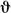между координатными линиями u = const, v = const в точке их пересечения имеет место формула

cos 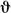= - F/√(EG).

Отсюда видно, что координатная сеть на поверхности ортогональна, если F = 0. Площадь поверхности также определяется первой квадратичной формой и для области Ω на поверхности вычисляется по формуле

S = ∫∫_Ω √(EG - F²) du dv.

Вторая квадратичная форма характеризует искривленность поверхности в пространстве. Именно, отношение второй квадратичной формы к первой

k = (L du² + 2M du dv + N dv²)/(E du² + 2F du dv = G dv²)

представляет собой кривизну плоского сечения, нормального к поверхности, проведенного в направлении du : dv (см. Нормальная кривизна поверхности). Существует простая связь между кривизной кривой, лежащей на поверхности, и кривизной нормального сечения поверхности, проведенного через касательную кривой (Менье теорема). Экстремальные значения нормальной кривизны поверхности в данной точке наз. главными кривизнами. Они достигаются по главным направлениям. Нормальная кривизна поверхности в произвольном направлении выражается через главные кривизны и углы, к-рые это направление образует с главными (Эйлера формула). Главные кривизны k₁ и k₂ определяются из уравнения

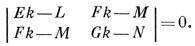
Их полусумма называется средней кривизной поверхности. Важный класс поверхностей составляют поверхности нулевой средней кривизны - так называемые минимальные поверхности. Они отличаются тем, что достаточно малый кусок такой поверхности имеет наименьшую площадь среди поверхностей с той же границей. Произведение К = k₁k₂ главных кривизн наз. гауссовой кривизной поверхности

K = (LN - M²)/(EG - F²).

Из этой формулы видно, что гауссова кривизна поверхности выражается через коэффициенты первой и второй квадратичных форм. Однако гауссову кривизну можно выразить через коэффициенты только первой формы и их производные (Гаусса теорема).

Две поверхности, между к-рыми может быть установлен гомеоморфизм, сохраняющий длины кривых, наз. изометричными поверхностями.

Коэффициенты первой и второй квадратичных форм независимы. Одно из соотношений между этими коэффициентами дает теорема Гаусса. Существуют еще два соотношения, открытые К. М. Петерсоном и Д. Кодацци (D. Codazzi) (см. Петерсона-Кодацци уравнения). Эти три соотношения составляют полную систему независимых соотношений между коэффициентами первой и второй квадратичных форм поверхности. Согласно Бонне теореме, если для двух дифференциальных квадратичных форм, из к-рых первая положительно определенная, выполнены соотношения Гаусса, Петерсона, Кодацци, то существует, и притом единственная, с точностью до положения в пространстве, поверхность, имеющая эти формы первой и соответственно второй квадратичными формами.

Раздел теория поверхностей, в к-ром изучаются свойства фигур на поверхности, зависящие только от измерения длин кривых на поверхности, наз. внутренней геометрией поверхностей. Так как длины кривых определяются первой квадратичной формой, то речь идет о таких свойствах, к-рые связаны только с первой квадратичной формой. В частности, объектами внутренней геометрии поверхностей являются длины кривых, углы между кривыми, площадь и гауссова кривизна. Важным понятием внутренней геометрии поверхности является понятие геодезической линии. Так называется линия, к-рая на достаточно малом участке является кратчайшей среди всех кривых на поверхности, соединяющих ее концы. Следующее важное понятие внутренней геометрии поверхности - понятие геодезической кривизны кривой. Гаусса - Бонне теорема связывает интеграл от гауссовой кривизны поверхности по площади, интеграл от геодезич. кривизны края по его длине и эйлерову характеристику.

Внутренняя геометрия поверхности может быть построена как геометрия двумерного метрич. многообразия, в к-ром расстояние между бесконечно близкими точками (u, v) и (u + du, v + dv) определяется с помощью заданной дифференциальной формы ds². При таком подходе к внутренней геометрии поверхности она допускает естественное обобщение, при к-ром заданное многообразие имеет любую размерность n, а метрика задается дифференциальной положительно определенной квадратичной формой и переменных ds² = g_αβdu^αdu^β. Дальнейшее обобщение состоит в отказе от положительной определенности формы ds². Это приводит к теории пространств общей теории относительности, в частности к Минковского пространствам. Если, наконец, отказаться и от квадратичной формы линейного элемента ds², а рассматривать общую положительную однородную форму первой степени от du^α, то получим Финслерово пространство. Еще более далеким обобщением внутренней геометрии поверхности является геометрия пространств со связностью данной группы, в частности геометрия пространств с аффинной связностью, проективной связностью и конформной связностью.

Лит.: [1] Вiаnсhi L., Lezioni di geometria differenziale, t. 1-2, 3 ed., Bologna, 1927 - 30; [2] Dаrbоux G., Lecons sur la théorie générale des surfaces et les applicatons geometriques du calcul infinitesimal, p. 1-4, 2 ed., P., 1894 - 1925; [3] Стройк Д. Дж., Очерк истории дифференциальной геометрии до XX столетия, пер. с англ., М.-Л., 1941; [4] Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956; [5] Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; [6] Бляшке В., Введение в дифференциальную геометрию, пер. с нем., М., 1957; [7] его же, Дифференциальная геометрия и геометрические основы теории относительности Эйнштейна, пер. с нем., т. 1, М.-Л., 1935; [8] Стернберг С., Лекции по дифференциальной геометрии, пер. с англ., М., 1970; [9] Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 1-2, М.-Л., 1947-48; [10] Шуликовский В. И., Классическая дифференциальная геометрия в тензорном изложении, М., 1963; [11] Схоутен И. А., Стройк Д. Дж., Введение в новые методы дифференциальной геометрии, пер. с англ., т. 1-2, М.-Л., 1939-1948; [12] Фиников С. П., Проективно-дифференциальная геометрия, М.-Л., 1937; [13] его же, Теория конгруэнции, М.-Л., 1950; [14] Широков П. А., Широков А. П., Аффинная дифференциальная геометрия, М., 1959; [15] Норден А. П., Пространства аффинной связности, М.-Л., 1950.

А. В. Погорелов.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.