ДИФФЕРЕНЦИАЛЬНАЯ АЛГЕБРА

ДИФФЕРЕНЦИАЛЬНАЯ АЛГЕБРА - раздел алгебры, изучающий объекты, в к-рых, наряду с операциями сложения и умножения, имеются операции дифференцирования: дифференциальные кольца, дифференциальные модули, дифференциальные поля, дифференциальные алгебраич. многообразия.

Один из основных объектов Д. а.- алгебра дифференциальных полиномов ℱ{Y₁, ..., Y_n}, являющаяся аналогом кольца многочленов в коммутативной алгебре (см. Расширение дифференциального поля). Каждой системе дифференциальных уравнений

F₁ = 0, ..., F_k = 0

ставится в соответствие совершенный дифференциальный идеал {F₁, ..., F_k}, порожденный этой системой в алгебре дифференциальных полиномов. Теорема Ритта-Рауденбаха о базисе утверждает, что таким образом получаются все совершенные дифференциальные идеалы (дифференциальный идеал I наз. совершенным, если из а_m ∈ I для нек-рого компонента неприводимого дифференциального полинома A ∈ ℱ{Y₁, ..., Y_n} компонентой для {F}. Точнее, пусть F, A ∈ ℱ{Y₁, ..., Y_n}, порядки F и А относительно Y_n равны m и l соответственно, A_j есть j-я производная от А и S - сепаранта для А. Существуют t ≥ 0 и r > 0 такие, что

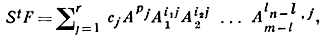
где p_j ≥ 0, i_kj ≥ 0, никакие два множества i_1j, ..., i_m-l,j не совпадают, порядок с_j относительно Y_n не превосходит l и c_j не делится на А. Если найдено такое разложение, то теорема о низких степенях гласит: общая компонента многообразия {А} является компонентой многообразия {F} тогда и только тогда, когда выписанное разложение содержит член c_kA^p_k, свободный от производных А, и степень к-рого ниже степени любого другого слагаемого в выписанном разложении, рассматриваемом как полином от А, А₁, ..., А_m-1 (в ненулевой характеристике это условие не является ни необходимым, ни достаточным).

Другое направление исследований в Д. а. представляет вопрос о расширении специализаций. Пусть (η₁, ..., η_n) и (ζ₁, ..., ζ_n) - точки в Uⁿ, где U - универсальное расширение дифференциального поля ℱ. Точка (ζ₁, ..., ζ_n) наз. дифференциальной специализацией точки (η₁, ..., η_n) над ℱ (что обозначается (η₁, ..., η_n) →_ℱ (ζ₁, ..., ζ_n), если любой дифференциальный полином, обращающийся в нуль в (η₁, ..., η_n), обращается в нуль и в (ζ₁, ..., ζ_n). Если (η₁, ..., η_n) →_ℱ (ζ₁, ..., ζ_n) и 1 ≤ k ≤ n, то очевидно, что (η₁, ..., η_t) →_ℱ (ζ₁, ..., ζ_t). Говорят, что первая специализация является расширением второй.

Пусть даны (η₁, ..., η_t) и k и пусть B ∈ ℱ{Y₁, ..., Y_t} таков, что B(η₁, ..., η_n) ≠ 0. Доказано, что существует ненулевой дифференциальный полином B₀ ∈ ℱ{Y₁, ..., Y_k}, удовлетворяющий условию B₀(η₁, ..., η_k) ≠ 0, и такой, что любая дифференциальная специализация (η₁, ..., η_k) →_ℱ (ζ₁, ..., ζ_k), для которой B₀(ζ₁, ..., ζ_t) ≠ 0, может быть расширена до дифференциальной специализации (η₁, ..., η_n) → (ζ₁, ..., ζ_n), где B(ζ₁, ..., ζ_n) ≠ 0. Однако, в отличие от ситуации в алгебраич. геометрии, дифференциальная специализация (η₁, ..., η_k) →_ℱ (ζ₁, ..., ζ_k) не всегда может быть расширена до дифференциальной специализации (η₁, ..., η_n) →_ℱ (ζ₁, ..., ζ_n) даже если элементы ζ_k+1, ..., ζ_n будут принимать значение ∞. Таким образом возникает задача: найти критерий, когда дифференциальная специализация (η₁, ..., η_k) →_ℱ (ζ₁, ..., ζ_k) может быть расширена до дифференциальной специализации (η₁, ..., η_n) →_ℱ (ζ₁, ..., ζ_n).

Частный случаи этой проблемы встречается в проблеме неопределенных форм. Пусть полиномы F, G ∈ ℱ{Y₁, ..., Y_n} взаимно простые, G ≠ 0, и F и G обращаются в нуль в точке (0, ..., 0). Проблема состоит в том, чтобы отношению F/G приписать значение в точке (0, ..., 0). Пусть элементы t₁, ..., t_n ∈ U дифференциально алгебраически независимы над ℱ и

u = F(t₁, ..., t_n)/G(t₁, ..., t_n).

Естественно сказать, что F/G допускает значение α в точке (0, ..., 0), если (t₁, ..., t_n, u) →_ℱ (0, ..., 0, α).

Таким образом проблема сводится к нахождению расширений (t₁, ..., t_n) →_ℱ (0, ..., 0) до (t₁, ..., t_n, u). Это эквивалентно определению элементов α ∈ U таких, что (0, ..., 0, α) является нулем общей компоненты дифференциального полинома Y_n+1G - F ∈ ℱ{Y₁, ..., Y_n+1}. Дж. Ритт (J. Ritt) предположил, что а либо определено однозначно (возможно, равно ∞), либо полностью произвольно; он доказал это предположение для обыкновенных дифференциальных полей при n = 1, ord(FG) = 1. Изучаются свойства конкретных дифференциальных идеалов в кольце ℱ{Y₁, ..., Y_n}. Для бесконечной последовательности Σ₁, ..., Σ_p, ... простых дифференциальных идеалов в ℱ{Y₁, ..., Y_n}, где каждый Σ_i - собственный делитель идеала Σ_i+1, пересечение всех Σ_i является простым дифференциальным идеалом и размерность соответствующего многообразия 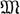больше размерности многообразия 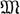_i, соответствующего Σ_i для любого i.

Из других результатов о дифференциально алгебраич. многообразиях следует отметить аналог теоремы Люрота: если 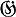расширение дифференциального поля ℱ, к-рое содержится в ℱ<u>, то 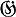содержит элемент v такой, что ℱ<v> = .

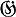Однако теория дифференциально алгебраич. кривых (многообразий дифференциальной размерности 1) находится в начальной стадии развития; даже для таких инвариантов, как род кривой в алгебраич. геометрии, дифференциально алгебраич. аналоги не найдены. Значительный интерес представляет теория пересечений дифференциально алгебраич. многообразий. Для них неверно утверждение, что пересечение двух нприводимых многообразий размерности р и q в n-мерном аффинном пространстве имеет размерность не менее p + q - n. Однако дифференциально алгебраич. многообразия, кроме размерности, характеризуются также порядком относительно выбранного базиса дифференциальной трансцендентности. Для порядка пересечения многообразий относительно специальным образом выбираемого базиса получены нек-рые оценки сверху. В аналитическом случае доказана следующая теорема о пересечении компонент одного дифференциального полинома: если F - дифференциальный полином от неизвестных Y₁, ..., Y_n, то нуль полинома F, содержащийся более яем в одной компоненте F, аннулирует ∂F/∂Y_ij для i = 1, ..., n и любого j. Понятия дифференциально алгебраич. многообразия можно обобщить (уже не предполагая его аффинным). В частности, можно ввести понятия дифференциально однородных полиномов и проективных дифференциально алгебраич. многообразий.

Для дифференциального поля F не существует дифференциально алгебраич. замыкания, не существует дифференциально алгебраич. замкнутых полей. Заменой их, в нек-ром смысле, являются так наз. «стесненные» расширения.

Одним из направлений в Д. а. является теория Галуа дифференциальных полей. Для дифференциального поля ℱ строится универсальное дифференциальное расширение U и рассматривается множество дифференциальных изоморфизмов конечно порожденного дифференциально алгебраич. расширения 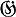поля ℱ в U, тождественных на ℱ. Если 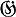является сильно нормальным расширением ℱ, то на множестве G дифференциальных изоморфизмов 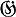в U можно ввести структуру алгебраич. группы над полем констант К поля U. Частным случаем сильно нормальных расширений являются расширения Пикара - Вессио, получающиеся присоединением к полю ℱ решений линейного однородного дифференциального уравнения с коэффициентами в поле ℱ. Группа Галуа расширения Пикара - Вессио является алгебраической матричной группой. Связь между промежутонными полями и подгруппами группы G описывается следующей теоремой.

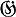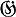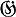Пусть - сильно нормальное расширение дифференциального поля ℱ с полем констант С. а) Если ℱ₁ -дифференциальное поле такое, что ℱ ⊂ ℱ₁ ⊂ , то сильно нормально над группа Галуа G(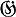/ℱ₁) является С-подгруппой в G(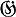/ℱ₁) и поле инвариантов группы C(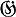/ℱ₁) в 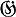совпадает с б) Если G₁ является С-подгруппой группы G(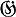/ℱ) и ℱ₁ обозначает множество инвариантов группы G₁ в 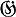, то ℱ₁ - дифференциальное поле, ℱ ⊂ ℱ₁ ⊂ 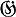и G(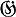/ℱ₁) = G₁.

Нормальным делителям С₁ группы G(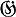/ℱ₁) соответствуют при этом сильно нормальные расширения ℱ₁ поля ℱ, и наоборот. Для связных разрешимых групп решена обратная задача Галуа, т. е. вопрос о существовании у поля ℱ сильно нормального расширения 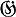, группа Галуа к-рого G(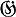/ℱ) изоморфна заданной группе. Эта задача сведена к оценке размерности нек-рого векторного пространства над полем констант С поля ℱ и ранга некоторой абелевой группы. Имеются результаты по теории Галуа бесконечных расширений. Смежными с теорией Галуа вопросами занимается теория интегрирования в конечном виде.

Разрабатывается теория дифференциальных алгебраич. групп, существенно отличающаяся от своего алгебраич. аналога. В частности, дифференциальное кольцо всюду определенных дифференциальных рациональных функций на аффинном дифференциальном алгебраич. множестве не является дифференциальным координатным кольцом, и в общем случае не конечно порождено как дифференциальная алгебра.

Среди результатов о приближении дифференциально алгебраич. функций рациональными может быть отмечен аналог теоремы Лиувилля о приближении алгебраич. чисел рациональными. Однако доказательство аналога теоремы Туэ - Зигеля - Рота остается (1978) проблемой.

Развивается теория колец с высшими дифференцированиями. При изучении объектов ненулевой характеристики высшие дифференцирования представляют более сильное средство. Если характеристика дифференциального кольца А равна р, то р-я степень любого элемента является константой, в то время как для колец с высшими дифференцированиями это не так. Для колец с высшими дифференцированиями получены аналоги многих перечисленных выше результатов, касающихся как теории пересечения идеалов, так и теории Галуа.

Лит.: [1] Капланский И., Введение в дифференциальную алгебру, пер. с англ., М., 1959; [2] Ritt J. F., Differential algebra, N. Y., 1950; [3] Kolchin E. R., Differential algebra and algebraic groups, N. Y.-L., 1973; [4] его жe, Some problems in differential algebra, в сб.: Тр. международного конгресса математиков. Москва 1966, М., 1968.

А. В. Михалев, Е. В. Панкратьев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.