ДИФФЕРЕНЦИАЛОВ МОДУЛЬ

ДИФФЕРЕНЦИАЛОВ МОДУЛЬ, модуль кэлеровых дифференциалов,- алгебраический аналог понятия дифференциала функции. Пусть А - коммутативное кольцо, рассматриваемое как алгебра над своим подкольцом В. Д. м. B-алгебры А определяется как фактормодуль Ω¹_A/B свободного А-модуля с базисом (dx)_x∈A по подмодулю, порожденному элементами вида

d(x + y) - dx - dy, d(xy) - xdy - ydx, db,

где x, y ∈ A, b ∈ B. Канонич. гомоморфизм A-модулей d: A → Ω¹_A/B является B-дифференцированием кольца А (см. Дифференцирование кольца) со значением в A-модуле Ω¹_A/B, обладающим следующим свойством универсальности: для любого S-дифференцирования ∂: А → М со значением в А-модуле М существует однозначно определенный гомоморфизм A-модулей ∂̅: Ω¹_A/B → М такой, что ∂̅ ○ ∂ = ∂. Соответствие ∂ → ∂̅ определяет изоморфизм А-модулей

Der_B(A, M) ≃ Hom_A(Ω¹_A/B, М).

В частности, модуль дифференцирований кольца А в себя изоморфен двойственному А -модулю к модулю Ω¹_A/B.

Если А ⊗_B А рассматривать как A-алгебру относительно гомоморфизма

А → А ⊗_B А (а → a ⊗ 1)

и I - идеал, порожденный элементами вида

а ⊗ 1 - 1 ⊗ a,

то А -модуль Ω¹_A/B изоморфен А -модулю I/I². Д. м. Ω¹ обладает следующими свойствами: 1) Если S - мультипликативно замкнутое множество в А и T = S ∩ B, то существует канонич. изоморфизм локализации

(Ω¹_A/B)_S ≅ Ω¹_AS/BT.

2) Если φ: А → А' - гомоморфизм B-алгебр, то определена каноническая точная последовательность А'-модулей:

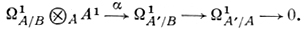
3) Если I - идеал кольца А и А' = А/I, то существует каноническая точная последовательность A'-модулей:

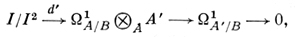
где гомоморфизм d' индуцирован дифференцированием d: A → Ω_A/B.

4) Поле К является сепарабельным расширением поля k конечной степени трансцендентности n в том и только в том случае, когда существует изоморфизм K-пространств Ω¹_K/k ≅ Kⁿ.

5) Если А = В [Т₁, ..., Т_n] - алгебра многочленов, то Ω¹_A/B свободный А -модуль с базисом dT₁, ..., dT_n.

6) Алгебра А конечного типа над совершенным полем k Является регулярным кольцом тогда и только тогда, когда А-модуль Ω¹_A/k проективен.

7) В свойстве 2) А -алгебра А' конечного типа является гладкой над А тогда п только тогда, когда гомоморфизм α инъективен, а Д. м. Ω¹_A'/A проективен и его ранг равен относительной размерности А' над А.

Внешняя степень ∧ⁱΩ¹_A/B Д. м. Ω¹_A/B наз. модулем дифференциальных i-форм В-алгебры А и обозначается Ωⁱ_A/B.

Свойство 1) позволяет для любого морфизма схем X → Y определить пучок относительных (или кэлеровых) дифференциалов Ω¹_X/Y и их внешние степени Ωⁱ_X/Y

Лит.: [1] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972; [2] Grothendieck A., Revêtements étales et groupe fondamentale, В.-Hdlb.-N. Y., 1971; [3] его же, «Publ. math. IHES», 1964, №20; [4] Kähler E., Algebra und Differentialrechmmg, В., 1958.

И. В. Долгачев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.