ДИФФЕРЕНЦИАЛ НА РИМАНОВОЙ ПОВЕРХНОСТИ

ДИФФЕРЕНЦИАЛ НА РИМАНОВОЙ ПОВЕРХНОСТИ - дифференциальная форма на римановой поверхности S, инвариантная относительно конформного преобразования локального униформизирующего параметра z = x + iy. Чаще всего встречаются дифференциалы (д.) первого порядка - это дифференциальные формы размерности 1, линейные относительно дифференциалов каждой из переменных (х, у), вида

ω = p dx + q dy ≡ p(x, y)dx + q(x, y)dy, π = r dx + s dy,

инвариантные относительно замены параметра, с достаточно гладкими коэффициентами р, q, ...; д. нулевого порядка - это достаточно гладкие комплексные функции f = f(x, у), g = g(x, у), инвариантные относительно замены параметра, т. е. функции точки Р ∈ S; д. второго порядка имеют вид

Ω = Adxdy = A(х, y)dxdy, П = Bdxdy.

Все д. на римановых поверхностях порядков k > 2 тождественно равны 0.

Сложение д. на римановых поверхностях одного и того же порядка определяется естественным путем:

f + g, ω + π = (p + r)dx + (q + s)dy, Ω + П = (A + B)dxdy;

оно коммутативно и ассоциативно. Внешнее умножение д. на римановых поверхностях дистрибутивно относительно сложения, обозначается знаком ∧ и определяется правилами:

f ∧ g = fg; f ∧ ω = (fp) dx + (fg) dy,

dx ∧ dx ≡ dy ∧ dy = 0, dy ∧ dx = -dx ∧ dy = -dx dy; отсюда

ω ∧ π =(ps - qr) dx dy, π ∧ ω = -ω ∧ π; f ∧ Ω = (fA) dx dy.

Вообще, при внешнем умножении д. порядка k на д. порядка l при k + l ≤ 2 получается д. порядка k + l, а при k + l > 2 - тождественный нуль. Линейный оператор дифференцирования d= ∂/∂x dx + ∂/∂y dy переводит д. порядка k в д. порядка k+1:

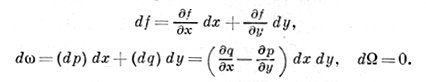
Кроме того,

d (fg) = f dg + g df, d (fω) = (df) ω + f(dω)= -ω(df) + f(dω)

и всегда dd = 0. Для д. на римановых поверхностях важен также линейный оператор звездного сопряжения

*ω = -q dx + р dy.

При этом

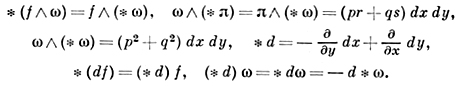
Оператор звездного сопряжения не совпадает с оператором комплексного сопряжения. Последний обозначается чертой: если f = g + ih, то f̅ = g - ih, ω̅ = p̅dx + q̅dy, Ω̅ = A̅dxdy; далее, dω̅ = dω̅, *ω̅ = *̅ω̅. Оператор Лапласа Δ = d * d определен на д. нулевого порядка:

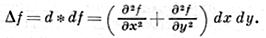
д., то ∫_c1ω= ∫_c2ω, т. е. периоды замкнутого д. зависят только от класса гомологий. Все периоды точного д. равны нулю. Обратно, замкнутый д. является точным тогда и только тогда, когда все его периоды равны 0.

Функция f ∈ C² наз. гармонической на S, если Δf = 0. Дифференциал ω ∈ C¹ наз. гармоническим дифференциалом на S, если ω замкнут и козамкнут, dω = d*ω = 0. Гармонич. д. ω является полным дифференциалом гармонич. функции в окрестности каждой точки P₀ ∈ S. Если действительные функции и, v ∈ C¹ на S связаны соотношением dv = *du, то они суть сопряженные гармонич. функции, удовлетворяющие условиям Коши — Римана. Следовательно, функция f = u + iv ∈ C¹ является регулярной аналитической, или голоморфной, на S, если *df = -idf. Дифференциал ω ∈ С¹ наз. регулярным аналитическим, или голоморфным, дифференциалом на S, если dω = 0 и *ω =— iω. Голоморфный д. ω является полным дифференциалом голоморфной функции в окрестности каждой точки P₀ ∈ S. Голоморфный д. ω представим локально в виде ω = fdz, где dz = dx + idy, а f — голоморфная функция от z.

Классы эквивалентности измеримых комплексных дифференциалов на римановой поверхности, для к-рых интеграл ∬_Sω ∧ (*ω̅) конечен, образуют гильбертово пространство L²(S) с обычным сложением, умножением на комплексные скаляры и скалярным произведением (ω, π) = ∬_S ω ∧ (*π̅). Каждый д. ω класса L²(S) ∩ С³(S) единственным образом представим в виде суммы ω = ω_h + df + *dg, где f, g ∈ C²(S) и ω_h — гармонический д. на римановой поверхности.

Рассмотренные выше гармонические и голоморфные функции или д. класса С¹ на S наз. регулярными на S. Пусть в проколотой окрестности U точки P₀ ∈ S определен д. θ, к-рый, напр., гармоничен в U. Тогда говорят, что гармонич. д. ω имеет особенность θ в Р₀, если разность ω — θ является регулярным гармонич. д.

Аналогичные определения применяются для гармонич. и аналитич. функций, аналитич. д. и т. п. В частности, в случае аналитического д. ω = fdz обычно предполагается, что функция f либо регулярная аналитическая в окрестности каждой точки P₀ ∈ S, либо имеет на S лишь изолированные особые точки однозначного характера. Аналитич. д. ω, имеющий на S только особенности в виде полюсов

θ = (a_-nz^-n + a_-n+1z^-n+1 + ... + a_-1z^-1) dz,

наз. мероморфным дифференциалом; при этом а_-n ≠ 0, n — порядок полюса, при n = 1 полюс наз. простым, а_-1 — вычет д. ω в полюсе Р₀. Мероморфные д. на компактной римановой поверхности S наз. абелевыми дифференциалами. Гармонич. функции на S или на нек-рой области D ⊂ S, имеющие заданные особенности, иногда наз. абелевыми потенциалами.

Интегрирование абелевых д. приводит к абелевым интегралам, исчерпывающим в сущности все интегралы от алгебраич. функций. При изучении аналитич. д. на произвольной, вообще говоря, некомпактной римановой поверхности S естественное требование сохранения основных черт классич. теории д. на компактных римановых поверхностях приводит к необходимости наложить на рассматриваемые регулярные д. дополнительные конформно инвариантные ограничения, наиболее употребительным из к-рых является условие интегрируемости, напр., аналитич. д. ω = fdz с квадратом, т. е. условие конечности интеграла Дирихле:

∬_S |f|² dxdy < +∞.

В теории д. на римановых поверхностях основное значение имеет проблема существования гармонич. и аналитич. д. с заданными особенностями на произвольной римановой поверхности S. С этим вопросом непосредственно связана проблема глобальной униформизации римановых поверхностей, т. к. построение глобальной униформизирующей требует именно умения строить д. с заданными особенностями.

Ниже приведены основные результаты по проблеме существования.

Если на S существует цикл с, не гомологичный нулю, то на S существует всюду регулярный гармонич. д.

ω с периодом ∫_c ω ≠ 0 и всюду регулярный аналитич.

д. ω + i*ω. Эти д. не являются точными, и поэтому при их интегрировании нельзя получить однозначных на S гармонич. или аналитич. функций. На компактной римановой поверхности S всякий гармонический и точный д. тождественно равен нулю. Напротив, на некомпактных римановых поверхностях существуют отличные от тождественного нуля всюду регулярные точные гармонические и голоморфные д.

Пусть Р₀ — любая фиксированная точка произвольной римановой поверхности S, n — любое натуральное число. Тогда существуют: точный гармонич. д. с особенностью d(1/zⁿ) в Р₀; точный действительный гармонич. д. с особенностью Re d(1/zⁿ) или lm d(1/zⁿ) в Р₀; гармонич. функция с особенностью 1/zⁿ в P₀; аналитич. д. с особенностью d(1/z²) в Р₀, у к-рого действительная часть есть точный д.

Пусть Р₀ и Р₁ — любые различные точки S. Тогда существуют: гармонич. или аналитич. д. на S с особенностями —dz/z в Р₀ и dz/z в Р₁; действительная гармонич. функция на S с особенностями - ln |z| в Р₀ и ln|z| в P₁.

Пусть Р₀, Р₁, ..., Р_n — любые попарно различные точки на S и с₀, с₁, ..., с_n — любые отличные от нуля комплексные числа такие, что c₀ + с₁ ... + с_n = 0. Существует гармонический или аналитический д. на S, всюду регулярный, кроме Р₀, Р₁, ..., Р_n, а в точках Р_j имеющий простые полюсы соответственно с вычетами с_j, j = 0, 1, ..., n.

Для жордановых областей D ⊂ S, т. е. таких областей, граница к-рых ∂D состоит из n непересекающихся жордановых кривых с₁, с₂, ..., с_n, возможно также решение Дирихле задачи.

Наиболее законченной является теория д. для компактных римановых поверхностей S. Пусть род S равен g. Векторное пространство ℌ регулярных гармонич. д. ω над полем комплексных чисел имеет размерность 2g. Если a₁b₁a₂b₂ ... a_gb_g — циклы канонич. базиса гомологии S, то в качестве канонич. базиса д. ℌ можно выбрать д. ω_i, i = 1, 2, ..., g, с периодом 1 вдоль а_i, а вдоль a_j, j ≠ i, и вдоль всех b_i — с периодом 0; далее, ω_g+i, i = 1, 2, ..., g, имеют период 1 вдоль b_i, а вдоль b_j, j ≠ i, и вдоль всех а_i — период 0. Любой гармонич. д. ω представляется в виде линейной комбинации

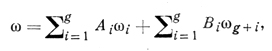
где А_i — так наз. А -периоды ω вдоль циклов а_i, a B_i суть B-периоды ω вдоль циклов b_i.

Голоморфные д. на компактной римановой поверхности наз. абелевыми дифференциалами первого рода. Размерность векторного пространства голоморфных д. равна g.

Все введенные выше д. на римановой поверхности можно выразить через переменные z и z̅, напр.:

f = f(z, z̅), ω = pdz + qdz̅ = р(z, z̅) dz + q(z, z̅) dz̅, Ω = A dz ∧ dz̅ - A(z, z̅) dz ∧ dz̅

и т. д. В отличие от комплексных многообразий высших размерностей, на римановых поверхностях нетривиальны только внешние дифференциальные формы типов (0, 0), (1, 0), (0, 1) и (1, 1), имеющие соответственно вид f, pdz, qdz̅, Adz ∧ dz̅. При этом аналитич. д. зависят только от z:

f = f(z), ω = p(z)dz.

Применяются также нелинейные дифференциальные формы вида p(z, z̅)dz^mdz̅ⁿ, где m и n - целые числа. Они также наз. дифференциалами типа (m, n), или размерности (m, n). При этом д. типа (0, 0) наз. функциями, типа (1, 0) - линейными дифференциалами, типа (-1, 0) - обратными дифференциалами, типа (2, 0) -квадратичными дифференциалами. Наибольшие применения получили квадратичные дифференциалы. См. также Глобальная структура траекторий, Локальная структура траекторий, Риманова поверхность, Униформизация.

Лит.: [1] Спрингер Дж., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [2] Неванлинна Р., Униформизация, пер. с нем., М., 1955; [3] Шиффер М., Спенсер Д. К., Функционалы на конечных римановых поверхностях, пер. с англ., М., 1957; [4] Behnke H., Sоmmеr F , Theorie der analytischen Funktionen einer komplexen veränderlichen, В., 1955.

E. Д. Соломенцев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.