ДИФРАКЦИИ МАТЕМАТИЧЕСКАЯ ТЕОРИЯ

ДИФРАКЦИИ МАТЕМАТИЧЕСКАЯ ТЕОРИЯ -раздел математич. физики, в к-ром изучаются задачи, возникающие при математич. описании волновых явлений. Такое определение Д. м. т. включает и геометрич. оптику, к-рую, однако, по традиции считают самостоятельным разделом математич. физики. Основные уравнения с частными производными, описывающие волновые процессы,- это Максвелла уравнения, уравнения динамических задач теории упругости, волновое уравнение (к-рое в случае двух пространственных переменных описывает колебания мембраны, а в случае трех пространственных переменных - распространение звука), уравнения гидродинамики и ряд других.

Постановка задач Д. м. т. может быть рассмотрена на примере волнового уравнения; задачи для других уравнений, описывающих волновые процессы, ставятся аналогично.

Нестационарные задачи дифракции - это, по существу, смешанные задачи, т. е. задачи с начальными и краевыми условиями для волнового уравнения

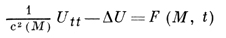
(1)

в области (0 < t < +∞) × Ω, где Ω - область на плоскости или в трехмерном пространстве; при этом

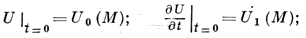
(2)

на границе S области Ω в простейших случаях

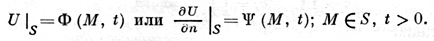
(3)

Здесь F, U₀, U₁, Ф, ψ - заданные функции. Иногда коэффициент с(М) на нек-рых поверхностях (в трехмерном случае) или линиях (в плоском случае) имеет скачки; тогда для U должны быть заданы еще и «условия сопряжения», связывающие значения функции U и ее производных по разные стороны поверхности, на к-рой с(М) имеет скачок. Корректность постановки задач такого рода доказывается при помощи априорных оценок искомого решения в различных нормах с использованием соображений компактности. Тонкие вопросы описания сингулярности решений, поведения решений при t → ∞, разработки практически применимых алгоритмов численного решения еще далеки от своего окончательного решения.

Стационарные задачи дифракции. Важную роль в Д. м. т. играют решения, гармонически зависящие от времени, т. е. решения уравнения (1), имеющие вид

U(М, t) = е^-iωtu(М), ω = const. (4)

Параметр ω соответствует частоте колебаний. Функции F(M, t), Ф(М, t) и ψ(M, t) [см. формулы (1) и (3)] тоже должны гармонически зависеть от времени:

F (М, t) = f(М)е^-iωt; Φ(М, t) = φ(M)e^-iωt;

Ψ(M, t) = ψ(M)e^-iωt,

Уравнение (1) и краевые условия (3) дают

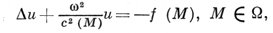
(5)

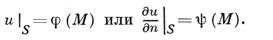
(6)

Для ограниченной области Ω большое значение имеет задача на отыскание нетривиальных решений уравнения (5) при f = 0 в случае однородных краевых условий φ(М) = 0 или ψ(M) = 0. Это - так наз. задача нахождения собственных функций. Однако основной интерес в Д. м. т. представляет решение уравнений (5) в случае краевых условий (6) при неограниченной области Ω. При этом условий (5) и (6) уже недостаточно для определения функции u: нужно задать еще «условия на бесконечности».

Наиболее часто задача дифракции ставится физически следующим образом: предполагается, что решение и уравнения (5) задается в виде суммы u_i + u_s двух функций, где u_i - известная функция («падающая волна»), a u_s - «отраженная» или возникшая в результате дифракции волна. Волна u_s не должна содержать в себе волн, идущих из бесконечности. Это физич. условие и приводит к вышеуказанным условиям на бесконечности. Соответствующие условия для случая, когда Ω есть внешность ограниченной области, ω > 0, с(М) вне сферы достаточно большого радиуса есть константа, а f(М) - финитная функция, наз. условиями излучения (см. Излучения условия). Задача (5), (6), при выполнении условий излучения, поставлена корректно, что доказывается путем сведения задачи к интегральным уравнениям или с помощью априорных оценок. Имеются также способы отбора единственного решения задачи (5), (6) с помощью принципа предельной амплитуды и принципа предельного поглощения. В случае, когда Ω, -внешность ограниченной области,- оба эти принципа выделяют те же решения, что и условия излучения. Сколько-нибудь общей теории задач для уравнения Гельмгольца в случае неограниченных областей не создано. Во всех практически важных случаях решения, представляющие физич. интерес, могут быть выделены при помощи принципа предельного поглощения.

В случае c(M) = const представление решений задач Дирихле (u|_S = φ(М)) и Неймана (∂u/∂n |_s = ψ) может быть получено в виде потенциалов соответственно двойного и простого слоев:

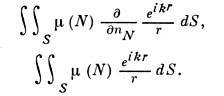
Для искомой плотности μ(N) получается интегральное уравнение Фредгольма 2-го рода. При проведении соответствующего доказательства разрешимости задач Дирихле и Неймана приходится преодолевать трудности, вполне аналогичные классич. трудности, возникающей при исследовании методами теории потенциала внешней задачи Дирихле для уравнения Лапласа.

Методы решения задач Д. м. т. Большое значение в задачах Д. м. т. имеет соотношение между длиной волны и характерными размерами тела, в окрестности к-рого изучается волновой процесс. Если длина волны велика (соответственно мала) по сравнению с характерными размерами тела, то говорят о дифракции длинных (соответственно коротких) волн. В случае дифракции длинных волн величина ω в уравнении (5) может рассматриваться как малый параметр. Это позволяет применять в длинноволновом случае различные варианты теории возмущений. В качестве первого приближения можно взять решение уравнения Лапласа. Кроме того, в длинноволновом случае для решения задач Д. м. т. применимы обычные численные методы математич. физики, напр., вариационный метод, численное решение интегральных уравнений теории потенциала. Для областей частного вида задачи Д. м. т. могут быть решены в явном виде, т. е. их решение представимо в виде рядов или интегралов, содержащих специальные функции. Наиболее важными приемами, позволяющими сделать это, являются метод разделения переменных, или Фурье метод, и Винера-Хопфа метод.

«Доведение до числа» явных решений задач Д. м. т. удавалось ранее лишь в длинноволновом случае (чем меньше длина волны, тем хуже сходятся ряды и интегралы). С развитием вычислительной техники стали поддаваться расчету многие задачи и в области, когда длина волны сравнима с характерными размерами неоднородности. Наиболее эффективными здесь являются методы сведений задач дифракции к интегральным и интегродифференциальным уравнениям и различные варианты проекционных методов.

Асимптотические методы Д. м. т. При малой длине волны численное решение дифракционной задачи весьма затруднительно, даже с использованием ЭВМ. Здесь на первый план выступают асимптотич. методы, к-рые представляют интерес еще и тем, что позволяют делать нек-рые общие заключения о рассматриваемой задаче. Под асимптотическими методами Д. м. т. понимаются нек-рые приемы нахождения приближенного выражения для искомых функций. Приемы эти базируются на физич. соображениях и формальных преобразованиях, чаще всего строго не обоснованных. Одним из первых приемов, позволяющих находить в виде нек-рой квадратуры приближенные решения коротковолновых задач дифракции, был Кирхгофа метод, широко применяющийся и теперь при решении прикладных задач. Не менее важное значение имеет лучевой метод, породивший целую серию приемов, позволяющих находить асимптотику многих дифракционных задач. Построения лучевого метода, как правило, бывает нетрудно провести, если соответствующее поле лучей регулярно. Если же оно имеет какие-либо особенности, то возникает ситуация, характерная для пограничного слоя теории: везде, кроме нек-рой весьма малой окрестности тех точек, где поле лучей теряет регулярность, асимптотика решений известна. Нужно найти ее только в этой малой области, т. е. в пограничном слое. Соответствующий аналог методики пограничного слоя получил название параболического уравнения метода. Он часто используется как для численного решения задач Д. м. т., так и для вывода асимптотич. формул.

Важные асимптотич. формулы для решения задач Д. м. т. могут быть получены в тех случаях, когда известно явное выражение для решения. Это явное решение по хорошо разработанной уже методике (так наз. метод Ватсона) преобразуют в контурный интеграл, асимптотика к-рого ищется либо применением перевала метода, либо теоремы о вычетах. Представляет интерес тот факт, что полученные на этом пути асимптотич. выражения иногда могут быть использованы как образец («эталон»), при помощи к-рого можно «угадывать» вид асимптотич. разложения в дифракционных задачах, явное решение к-рых неизвестно. Именно такие построения характерны для «метода эталонных задач», к-рый является дальнейшим развитием метода параболич. уравнения.

Лит.: [1] Бабич В. М., Булдырев В. С., Асимптотические методы в задачах дифракции коротких волн, М., 1972; [2] Вайнштейн Л. А., Теория дифракции и метод факторизации, М., 1966; [3] Никольский В. В., Вариационные методы для решения внутренних задач электродинамики, М., 1967; [4] Купрадзе В. Д., Граничные задачи теории колебаний и интегральные уравнения, М.-Л., 1950; [5] Купрадзе В. Д. и др., Трехмерные задачи математической теории упругости, 2 изд., М., 1976; [6] Фридлендер Ф., Звуковые импульсы, пер. с англ., М., 1962; [7] Xёнл X., Мауэ А., Вестпфаль К., Теория дифракции, пер. с нем., М., 1964; [8] Свешников А. Г., в кн.: International congress of mathematicians, Vancouver, 1974, p. 29-30.

В. M. Бабич.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.