ДИСПЕРСИЯ

ДИСПЕРСИЯ в теории вероятностей -мера ⅮX отклонения случайной величины X от ее математич. ожидания ЕX, определяемая равенством:

ⅮX = Е(X - ЕX)². (1)

Свойства Д.:

ⅮX = ЕX² - (ЕX)².

если с - действительное число, то

Ⅾ(cX) = c²ⅮX,

в частности Ⅾ(-X) = Ⅾ(X).

Когда говорят о Д. случайной величины X, всегда предполагают, что существует математич. ожидание ЕX; при этом Д. ⅮX может существовать (т. е. быть конечной) или не существовать (т. е. быть бесконечной). В современной теории вероятностей математич. ожидание случайной величины определяется через интеграл Лебега по пространству элементарных событий. Однако важную роль играют формулы, выражающие математич. ожидание различных функций от случайной величины X через распределение этой случайной величины на множестве действительных чисел (см. Математическое ожидание). Для Д. ⅮX эти формулы имеют вид:

a) ⅮX = ∑_i (a_i - EX)² p_i

для дискретной случайной величины X, принимающей не более чем счетное число различных значений а_i с вероятностями р_i = Р{X = a_i};

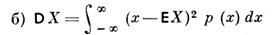
для случайной величины X, имеющей плотность распределения вероятностей р(х);

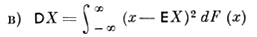
в общем случае, где F(x) - функция распределения случайной величины X и интеграл понимается в смысле Лебега-Стилтьеса или Римана-Стилтьеса.

Д. не является единственной мыслимой мерой отклонения случайной величины от ее математич. ожидания. Возможны другие меры отклонения, устроенные по тому же принципу, напр. Е|X - ЕX|, Е(X - ЕX)⁴ и т. д., а также меры отклонения, основанные на квантилях. Особая важность Д. объясняется главным образом той ролью, к-рую играет это понятие для предельных теорем. Грубо говоря, оказывается, что если знать математич. ожидание и Д. суммы большого числа случайных величин, то можно полностью определить закон распределения этой суммы: он оказывается нормальным (приблизительно) с соответствующими параметрами (см. Нормальное распределение).

Таким образом, важнейшие свойства Д. связаны с выражением для Д. Ⅾ(X₁ + ... + X_n) суммы случайных величин X₁, ..., X_n:

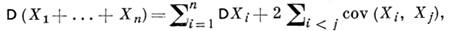
где

cov (X_i, X_j) = E{(X_i - ЕX_i)(X_j - EX_j)}

обозначает ковариацию случайных величин X_i и X_j. Если случайные величины X₁, ..., X_n попарно независимы, то cov(X_i, X_j) = 0. Поэтому для попарно независимых случайных величин

Ⅾ(X₁ + ... + Х_n) = ⅮX₁+ ... +ⅮX_n. (2)

Обратное утверждение неверно: из (2) не следует независимость. Однако, как правило, применение формулы (2) базируется на независимости случайных величин. Строго говоря, для справедливости (2) достаточно лишь, чтобы cov(X_i, X_j) = 0, т. е. чтобы случайные величины X₁, ..., X_n были попарно некоррелированы.

Применения понятия Д. развиваются по следующим двум направлениям. Во-первых, применения в области предельных теорем теории вероятностей. Если последовательность случайных величин X₁, X₂, ..., X_n, ... обладает тем свойством, что ⅮX_n → 0 при n → ∞, то для любого ε > 0 при n → ∞

Р{|X_n - EX_n| > ε} → 0

(см. Чебышева неравенство), т. е. практически при больших n случайная величина Х_n совпадает с неслучайной величиной ЕX_n. Развитие этих соображений приводит к доказательству закона больших чисел (см. Больших чисел закон), к доказательству состоятельности оценок (см. Состоятельная оценка) в математич. статистике, а также к иным применениям, в к-рых устанавливается сходимость по вероятности случайных величин. Другое применение в области предельных теорем связано с понятием нормировки. Нормировка случайной величины X производится путем вычитания математич. ожидания и деления на среднее квадратичное отклонение √ⅮX, иными словами, рассматривается величина Y = (X - ЕX) /√X. Нормировка последовательности случайных величин обычно необходима для получения сходящейся последовательности законов распределения, в частности сходимости к нормальному закону с параметрами 0 и 1. Во-вторых, применение понятия Д. в математич. статистике при обработке выборок. Если смотреть на случайную величину как на реализацию случайного эксперимента, то произвольное изменение шкалы отсчета приведет к преобразованию случайной величины X в величину Y = σX + a, где а - любое действительное число, σ - положительное число. Поэтому часто имеет смысл рассматривать не один теоретич. закон распределения F(x) случайной величины X, а тип законов, т. е. семейство законов распределения вида F((x - a)/σ), зависящих по крайней мере от двух параметров а и σ. Если EX = 0, ⅮX = 1, то EY = a, ⅮY = σ². Поэтому параметры теоретич. закона имеют следующий смысл a = EY и σ = √ⅮY. Отсюда вытекает способ определения этих параметров по выборке.

Лит.: [1] Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969; [2] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., т. 1-2, М., 1964-67; [3] Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975.

В. Н. Тутубалин.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.