ДИСПЕРСИОННЫЙ АНАЛИЗ

ДИСПЕРСИОННЫЙ АНАЛИЗ в математической статистике - статистический метод, предназначенный для выявления влияния отдельных факторов на результат эксперимента, а также для последующего планирования аналогичных экспериментов. Первоначально Д. а. был предложен Р. Фишером [1] для обработки результатов агрономия, опытов по выявлению условий, при к-рых испытываемый сорт сельскохозяйственной культуры дает максимальный урожай. Современные приложения Д. а. охватывают широкий круг задач экономики, социологии, биологии и техники и трактуются обычно в терминах статистич. теории выявления систематич. различий между результатами непосредственных измерений, выполненных при тех или иных меняющихся условиях.

Если значения неизвестных постоянных a₁, ... , а_I могут быть измерены с помощью различных методов или измерительных средств M₁, ... , M_J, и в каждом случае систематич. ошибка b_ij может, вообще говоря, зависеть как от выбранного метода M_j, так и от неизвестного измеряемого значения а_i, то результаты таких измерений представляют собой суммы вида

x_ijk = a_i + b_ij + y_ijk, i = 1, ..., I; j = 1, ..., J, k = 1, ..., K,

где K' - количество независимых измерений неизвестной величины а_i методом M_j, a y_ijk - случайная ошибка к-то измерения величины а_i методом М_j (предполагается, что все y_ijk - независимые одинаково распределенные случайные величины, имеющие нулевое математич. ожидание: ∃y_ijk = 0). Такая линейная модель наз. двухфакторной схемой Д. а.; первый фактор - истинное значение измеряемой величины, второй - метод измерения, причем в данном случае для каждой возможной комбинации значений первого и второго факторов осуществляется одинаковое количество K независимых измерений (это допущение для целей Д. а. не является существенным и введено здесь лишь ради простоты изложения).

Примером подобной ситуации могут служить спортивные соревнования I спортсменов, мастерство к-рых оценивается J судьями, причем каждый участник соревнований выступает K раз (имеет K «попыток»). В этом случае а_i - истинное значение показателя мастерства спортсмена с номером i, b_ij - систематич. ошибка, вносимая в оценку мастерства i-го спортсмена судьей с номером j, х_ijk - оценка, выставленная j-м судьей i-му спортсмену после выполнений последним k-й попытки, а у_ijk - соответствующая случайная погрешность. Подобная схема типична для так наз. субъективной экспертизы качества нескольких объектов, осуществляемой группой независимых экспертов. Другой пример -статистич. исследование урожайности сельскохозяйственной культуры в зависимости от одного из I сортов почвы и J методов ее обработки, причем для каждого сорта i почвы и каждого метода обработки с номером j осуществляется k независимых экспериментов (в этом примере b_ij - истинное значение урожайности для i-го сорта почвы при j-м способе обработки, х_ijk - соответствующая экспериментально наблюдаемая урожайность в k-м опыте, a y_ijk - ее случайная ошибка, возникающая из-за тех или иных случайных причин; что же касается величин а_i, то в агрономич. опытах их разумно считать равными нулю).

Положим с_ij = а_i + b_ij, и пусть с_i*, с_*j и с_** - результаты осреднений с_ij по соответствующим индексам, т. е.

c_i* = 1/J ∑_j c_ij,

Пусть, кроме того, α = c_**, β_i = c_i* - с_**, γ_i = с_*j - с_** и δ_ij = c_ij - c_i* - c_*j + c_**. Идея Д. а. основана на очевидном тождестве

c_ij = α + β_i + γ_i + δ_ij, i = 1, ..., I, j = 1, ..., J. (1)

Если символом (с_i) обозначить вектор размерности IJ, получаемый из матрицы ||с_ij|| порядка I × J с помощью какого-либо заранее фиксированного способа упорядочивания ее элементов, то (1) можно записать в виде равенства

(c_ij) = (α_ij) + (β_ij) + (γ_ij) + (δ_ij), (2)

где все векторы имеют размерность IJ, причем α_ij = α, β_ij = β_i, γ_ij = γ_j. Так как четыре вектора в правой части (2) ортогональны, то α_ij = α - наилучшее приближение функции с_ij от аргументов i и j постоянной величиной [в смысле минимальности суммы квадратов отклонений

∑_ij(c_ij - α)²]. В том же смысле α_ij + β_ij = α + β - наилучшее приближение c_ij функцией, зависящей лишь от i, α_ij + γ_ij = α + γ_j - наилучшее приближение с_ij функцией, зависящей лишь от j, а α_ij + β_ij + γ_ij = α + β_i + γ_j - наилучшее приближение с_ij суммой функций, из к-рых одна (напр., α + β_i) зависит лишь от i, а другая - лишь от j. Этот факт, установленный Р. Фишером (см. [1]) в 1918, позднее послужил основой теории квадратичных приближений функций.

В примере, связанном со спортивными соревнованиями, функция δ_ij выражает «взаимодействие» i-го спортсмена и j-го судьи (положительное значение δ_ij означает «подсуживание», т. е. систематич. завышение j-м судьей оценки мастерства i-го спортсмена, а отрицательное значение δ_ij означает «засуживание», т. е. систематич. снижение оценки). Равенство всех δ_ij нулю - необходимое требование, к-рое надлежит предъявлять к работе группы экспертов. В случае же агрономич. опытов такое равенство рассматривается как гипотеза, подлежащая проверке по результатам экспериментов, поскольку основная цель здесь - отыскание таких значений i и j, при к-рых функция (1) достигает максимального значения. Если эта гипотеза верна, то

max с_ij = α + max β_i + max γ_j,

и значит, выявление наилучших «почвы» и «обработки» может быть осуществлено раздельно, что приводит к существенному сокращению числа экспериментов (напр., можно при каком-либо одном способе обработки испытать все I сортов «почвы» и определить наилучший сорт, а затем на этом сорте опробовать все J способов «обработки» и найти наилучший способ; общее количество экспериментов с повторениями будет равно (I + J) K). Если же гипотеза {все δ_ij = 0} неверна, то для определения max c_ij необходим описанный выше «полный план», требующий при K повторениях IJK экспериментов.

В ситуации спортивных соревнований функция γ_ij = γ_j может трактоваться как систематич. ошибка, допускаемая j-м судьей по отношению ко всем спортсменам. В конечном счете γ_j - характеристика «строгости» или «либеральности» j-го судьи. В идеале хотелось бы, чтобы все γ_j были нулевыми, но в реальных условиях приходится мириться с наличием ненулевых значений γ_j и учитывать это обстоятельство при подведении итогов экспертизы (напр., за основу сравнения мастерства спортсменов можно принять не последовательности истинных значений α + β₁ + γ_j, ..., α + β_I + γ_j, а лишь результаты упорядочиваний этих чисел по их величине, поскольку при всех j = 1, ..., J такие упорядочивания будут одинаковыми). Наконец, сумма двух оставшихся функций α_ij + β_ij = α + β_i зависит лишь от i и поэтому может быть использована для характеризации мастерства i-го спортсмена. Однако здесь нужно помнить, что α + β_i = a_i + b_i* ≠' a_i. Поэтому упорядочивание всех спортсменов по значениям α + β_i (или по α + β_i + γ_j при каждом фиксированном j) может не совпадать с упорядочиванием по значениям a_i. При практической обработке экспертных оценок этим обстоятельством приходится пренебрегать, так как упомянутый полный план экспериментов не позволяет оценивать отдельно а_i и b_i*. Таким образом, число α + β_i = а_i + b_i, характеризует не только мастерство i'-го спортсмена, но и в той или иной мере отношение экспертов к этому мастерству. Поэтому, напр., результаты субъективных экспертных оценок, осуществленных в разное время (в частности, на нескольких Олимпийских играх), едва ли можно считать сопоставимыми. В случае же агрономич. опытов подобные трудности не возникают, поскольку все a_i = 0 и значит, α + β_i = b_i*.

Истинные значения функций α, β_i, γ_i и δ_ij неизвестны и выражаются в терминах неизвестных функций с_ij. Поэтому первый этап Д. а. заключается в отыскании статистич. оценок для с_ij по результатам наблюдений x_ijk. Несмещенная и имеющая минимальную дисперсию линейная оценка для с_ij выражается формулой

ĉ_ij = x_ij* = 1/K ∑_k X_ijk.

Так как α, β_i, γ_j и δ_ij - линейные функции от элементов матрицы ||с_ij||, то несмещенные линейные оценки для этих функций, имеющие минимальную дисперсию, получаются в результате замены аргументов с_ij соответствующими оценками, с̂_ij, т. е.

α̂ = x_***, β̂_i = x_i** - x_***, γ̂_j = x_*j* - x_***, δ̂_ij = x_ij* - x_i** - x_*j* + x_***,

причем случайные векторы (α̂_ij), (β̂_ij), (γ̂_ij) и (δ̂_ij), определенные так же, как введенные выше (α_ij), (β_ij), (γ_ij) и (δ_ij), обладают свойством ортогональности, и значит, они представляют собой некоррелированные случайные векторы (иными словами, любые две компоненты, принадлежащие разным векторам, имеют нулевой коэффициент корреляции). Кроме того, любая разность вида

x_ijk - x_ij* = x_ijk - ĉ_ij

некоррелирована с любой из компонент этих четырех векторов. Рассмотрим пять совокупностей случайных

величин {x_ijk}, {x_ijk - x_ij*}, {β̂_i}, {γ̂_j} и {δ̂_ij}. Так как x_ijk - x_ij* = y_ijk - _ij*, β̂_i = β_i + (y_i** - y_***), γ̂_i = γ_j + (y_*j* - y_***), δ̂_ij = δ_ij + (y_ij* - y_i** - y_*j* + y_***),

то дисперсии эмпирич. распределений, соответствующих указанным совокупностям, выражаются формулами

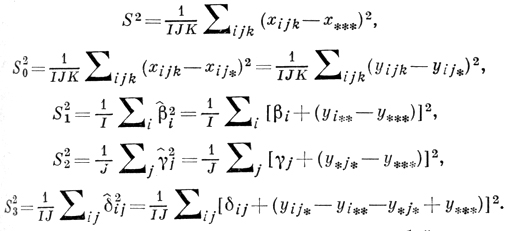
Эти эмпирич. дисперсии представляют собой суммы квадратов случайных величин, любые две из к-рых не-коррелированы, если только они принадлежат разным суммам; при этом относительно всех y_ijk справедливо тождество

S² = S²₀ + S²₁ + S²₂ + S²₃,

объясняющее происхождение термина «Д. а.». Пусть I, J, K > 2 и пусть

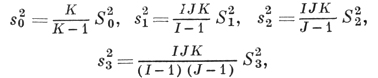
в таком случае

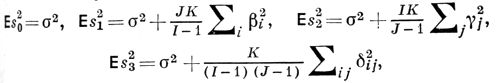
где σ² - дисперсия случайных ошибок y_ijk.

На основе этих формул и строится второй этап Д. а., посвященный выявлению влияния первого и второго факторов на результаты эксперимента (в агрономич. опытах первый фактор - сорт «почвы», второй - способ «обработки»). Напр., если требуется проверить гипотезу отсутствия «взаимодействия» факторов, к-рая выражается равенством ∑_ij δ²_ij = 0, то разумно вычислить дисперсионное отношение s²₃/s²₀ = F₃. Если это отношение значимо отличается от единицы, то проверяемая гипотеза отвергается. Точно так же для проверки гипотезы ∑_jγ²_j = 0 полезно отношение s²₂/s²₀ = F₂, к-рое надлежит также сравнить с единицей; если при этом известно, что ∑_ijδ²_ij = 0, то вместо F₂ целесообразно сравнить с единицей отношение

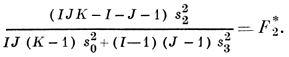
Аналогичным образом можно построить статистику, позволяющую дать заключение о справедливости или ложности гипотезы ∑_i β²_i = 0.

Точный смысл понятия значимого отличия указанных отношений от единицы может быть определен лишь с учетом закона распределения случайных ошибок у_ijk. В Д. а. наиболее обстоятельно изучена ситуация, в к-рой все y_ijk распределены нормально. В этом случае (α̂_ij), (β̂_ij), (γ̂_ij), (δ̂_ij) -независимые случайные векторы, а s²₀, s²₁, s²₂, s²₃ - независимые случайные величины, причем отношения

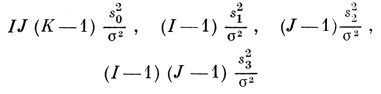
подчиняются нецентральным распределениям хи-квад-рат с f_m степенями свободы и параметрами нецентральности λ_m, m = 0, 1, 2, 3, где

f₀ = IJ(K - 1), f₁ = I - 1, f₂ = J - 1, f₃ = (I - J)(J - 1); λ₀ = 0, λ₁ = JK ∑_i β²_i/σ², λ₂ = IK ∑_j γ²_j/σ², λ₃ = K ∑_ij δ²_ij/σ².

Если параметр нецентральности равен нулю, то нецентральное распределение хи-квадрат совпадает с обычным распределением хи-квадрат. Поэтому в случае справедливости гипотезы λ₃ = 0 отношение s²₃/s²₀ = F₃ подчиняется F-распределению (распределению дисперсионного отношения) с параметрами f₃ и f₀. Пусть х - такое число, для к-рого вероятность события {F₃ > x} равна заданному значению ε, называемому уровнем значимости (таблицы функции х = х(ε; f₃, f₀) имеются в большинстве пособий по математич. статистике). Критерием для проверки гипотезы λ₃ = 0 служит правило, согласно к-рому эта гипотеза отвергается, если наблюдаемое значение F₃ превышает x; в противном случае гипотеза считается не противоречащей результатам наблюдений. Аналогичным образом конструируются критерии, основанные на статистиках F₂ и F^*₂.

Дальнейшие этапы Д. а. существенно зависят не только от реального содержания конкретной задачи, но также и от результатов статистич. проверки гипотез на втором этапе. Напр., в условиях агрономич. опытов справедливость гипотезы λ₃ = 0, как указано выше, позволяет более экономно спланировать аналогичные дальнейшие эксперименты (если помимо гипотезы λ₃ = 0 справедлива также и гипотеза λ₂ = 0, то это означает, что урожайность зависит лишь от сорта «почвы», и поэтому в дальнейших опытах можно воспользоваться схемой однофакторного Д. а.); если же гипотеза λ₃ = 0 отвергается, то разумно проверить, нет ли в данной задаче неучтенного третьего фактора? Если сорта «почвы» и способы ее «обработки» варьировались не в одном и том же месте, а в различных географич. зонах, то таким фактором могут быть климатич. или географич. условия, и «обработка» наблюдений потребует применения трехфакторного Д. а.

В случае экспертных оценок статистически подтвержденная справедливость гипотезы λ₃ = 0 дает основание для упорядочивания сравниваемых объектов (напр., спортсменов) по значениям величин α̂ + α̂_i, i = 1, ..., I. Если же гипотеза λ₃ = 0 отвергается (в задаче о спортивных соревнованиях это означает статистич. обнаружение «взаимодействия» нек-рых спортсменов и судей), то естественно попытаться перевычислить все результаты заново, предварительно исключив из рассмотрения x_ijk с такими парами индексов (i, j), для к-рых абсолютные значения статистич. оценок δ_ij превышают нек-рый заранее установленный допустимый уровень. Это означает, что из матрицы ||x_ij*|| вычеркиваются нек-рые элементы, и значит, план Д. а. становится неполным.

Модели современного Д. а. охватывают широкий круг реальных экспериментальных схем (напр., схемы неполных планов, со случайно или неслучайно отобранными элементами x_ij*). Соответствующие этим схемам статистич. выводы во многих случаях находятся в стадии разработки. В частности, еще (к 1978) далеки от окончательного решения те задачи, в к-рых результаты наблюдений x_ijk = c_ij + y_ijk не являются одинаково распределенными случайными величинами; еще более трудная задача возникает в случае зависимости величин x_ijk. Неизвестно решение проблемы выбора факторов (даже в линейном случае). Суть этой проблемы заключается в следующем: пусть с = с(u, v) - непрерывная функция и пусть u = u(z, w) и v = v(z, w) - какие-либо линейные функции от переменных z и w. Фиксируя значения z₁, ..., z_I и w₁, ..., w_J, можно при каждом заданном выборе линейных функций u и v определить с_ij формулой

с_ij = с[u(z_i, w_j), v(z_i, w_j)]

и построить Д. а. этих величин по результатам соответствующих наблюдений х_ijk. Проблема заключается в отыскании таких линейных функций u и v, к-рым соответствует минимальное значение суммы квадратов ∑_ij δ²_ij, где

δ_ij = c_ij - c_i* - c_*j + c_**

(предполагается, что функция с(u, v) неизвестна). В терминах Д. а. эта проблема сводится к статистич. отысканию таких факторов z = z(u, v) и w = w(u, v), к-рым соответствует «наименьшее взаимодействие».

Лит.: [1] Fisher R. A., Statistical methods for research workers, Edinburgh, 1925; [2] Шеффе Г., Дисперсионный анализ, пер. с англ., М., 1963; [3] Xальд А., Математическая статистика с техническими приложениями, пер. с англ., М., 1956; [4] Снедекор Дж. У., Статистические методы в применении к исследованиям в сельском хозяйстве и биологии, пер. с англ., М., 1961.

Л. Н. Большев.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.