ДИСПЕРСИОННОЕ СООТНОШЕНИЕ

ДИСПЕРСИОННОЕ СООТНОШЕНИЕ - соотношение, связывающее нек-рые величины, характеризующие рассеяние частиц, с величинами, характеризующими их поглощение. Более точно, Д. с.- это соотношение, связывающее эрмитову часть амплитуды рассеяния (в более общем случае - Грина функции) с определенного рода интегралами от ее антиэрмитовой части. Пусть функция f(t) абсолютно интегрируема на оси и удовлетворяет условию причинности f(t) = 0, t < 0. Тогда ее преобразование Фурье - Лапласа

f̃(ζ) = ∫ f(t) e^iζt dt, ζ = p + iq,

есть голоморфная функция в верхней полуплоскости q > 0, а действительная и мнимая части граничного значения f̃(p) удовлетворяют Д. с.

  (*)

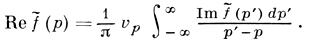При описании реальных физич. процессов Д. с. типа (*) усложняются, так как функция f̂(ζ) может расти на ∞ как многочлен (в этом случае получают Д. с. с вычитаниями), граничное значение f̃(p) может быть обобщенной функцией медленного роста, а число переменных - больше одного (многомерные Д. с).

Лит.: [1] Боголюбовы. Н., Медведев Б. В., Поливанов М. К., Вопросы теории дисперсионных соотношений, М., 1958; [2] Владимиров В. С., Обобщенные функции в математической физике, М., 1976.

В. С. Владимиров.

Источники:

1. Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 2 Д - Коо.-М.: «Советская Энциклопедия», 1979.-1104 стб., ил.